Advertisements
Advertisements
प्रश्न
A source emitting light of wavelengths 480 nm and 600 nm is used in a double-slit interference experiment. The separation between the slits is 0.25 mm and the interference is observed on a screen placed at 150 cm from the slits. Find the linear separation between the first maximum (next to the central maximum) corresponding to the two wavelengths.
उत्तर
Given
Wavelengths of the source of light,
\[\lambda_1 = 480 \times {10}^{- 9} m\text{ and }\lambda_2 = 600 \times {10}^{- 9} m\]
Separation between the slits,
\[d = 0 . 25 mm = 0 . 25 \times {10}^{- 3} m\]
Distance between screen and slit,
\[D = 150 cm = 1 . 5 m\]
We know that the position of the first maximum is given by
\[y = \frac{\lambda D}{d}\]
So, the linear separation between the first maximum (next to the central maximum) corresponding to the two wavelengths = y2 − y1
\[y_2 - y_1 = \frac{D\left( y_2 - y_1 \right)}{d}\]
\[\Rightarrow y_2 - y_1 = \frac{1 . 5}{0 . 25 \times {10}^{- 3}}\left( 600 \times {10}^{- 9} - 480 \times {10}^{- 9} \right)\]
\[ y_2 - y_1 = 72 \times {10}^{- 5} m = 0 . 72 mm\]
APPEARS IN
संबंधित प्रश्न
In Young' s experiment the ratio of intensity at the maxima and minima . in the interference pattern is 36 : 16. What is the ratio of the widths of the two slits?
In young’s double slit experiment, deduce the conditions for obtaining constructive and destructive interference fringes. Hence, deduce the expression for the fringe width.
In a double-slit experiment using the light of wavelength 600 nm, the angular width of the fringe formed on a distant screen is 0.1°. Find the spacing between the two slits.
In a Young’s double-slit experiment, the slits are separated by 0.28 mm and the screen is placed 1.4 m away. The distance between the central bright fringe and the fourth bright fringe is measured to be 1.2 cm. Determine the wavelength of light used in the experiment.
In Young’s double slit experiment using monochromatic light of wavelength λ, the intensity of light at a point on the screen where path difference is λ, is K units. Find out the intensity of light at a point where path difference is λ/3.
A double slit S1 − S2 is illuminated by a coherent light of wavelength \[\lambda.\] The slits are separated by a distance d. A plane mirror is placed in front of the double slit at a distance D1 from it and a screen ∑ is placed behind the double slit at a distance D2 from it (see the following figure). The screen ∑ receives only the light reflected by the mirror. Find the fringe-width of the interference pattern on the screen.
In a Young's double slit experiment, the separation between the slits = 2.0 mm, the wavelength of the light = 600 nm and the distance of the screen from the slits = 2.0 m. If the intensity at the centre of the central maximum is 0.20 W m−2, what will be the intensity at a point 0.5 cm away from this centre along the width of the fringes?
Consider the arrangement shown in the figure. By some mechanism, the separation between the slits S3 and S4 can be changed. The intensity is measured at the point P, which is at the common perpendicular bisector of S1S2 and S2S4. When \[z = \frac{D\lambda}{2d},\] the intensity measured at P is I. Find the intensity when z is equal to

(a) \[\frac{D\lambda}{d}\]
(b) \[\frac{3D\lambda}{2d}\] and
(c) \[\frac{2D\lambda}{d}\]
What should be the path difference between two waves reaching a point for obtaining constructive interference in Young’s Double Slit experiment ?
When a beam of light is used to determine the position of an object, the maximum accuracy is achieved, if the light is ______.
"If the slits in Young's double slit experiment are identical, then intensity at any point on the screen may vary between zero and four times to the intensity due to single slit".
Justify the above statement through a relevant mathematical expression.
Two slits in Young's interference experiment have width in the ratio 1 : 2. The ratio of intensity at the maxima and minima in their interference is ______.
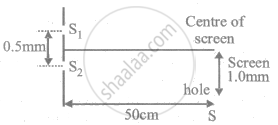
In Young's double slit experiment shown in figure S1 and S2 are coherent sources and S is the screen having a hole at a point 1.0 mm away from the central line. White light (400 to 700 nm) is sent through the slits. Which wavelength passing through the hole has strong intensity?
ASSERTION (A): In an interference pattern observed in Young's double slit experiment, if the separation (d) between coherent sources as well as the distance (D) of the screen from the coherent sources both are reduced to 1/3rd, then new fringe width remains the same.
REASON (R): Fringe width is proportional to (d/D).
Using Young’s double slit experiment, a monochromatic light of wavelength 5000Å produces fringes of fringe width 0.5 mm. If another monochromatic light of wavelength 6000Å is used and the separation between the slits is doubled, then the new fringe width will be ______.
The maximum number of possible interference maxima for slit-separation equal to twice the wavelength in Young's double-slit experiment is ______.
- Assertion (A): In Young's double slit experiment all fringes are of equal width.
- Reason (R): The fringe width depends upon the wavelength of light (λ) used, the distance of the screen from the plane of slits (D) and slits separation (d).
In Young's double-slit experiment, the separation between the two slits is d and the distance of the screen from the slits is 1000 d. If the first minima fall at a distance d from the central maximum, obtain the relation between d and λ.
