Advertisements
Advertisements
प्रश्न
In Young’s double slit experiment to produce interference pattern, obtain the conditions for constructive and destructive interference. Hence deduce the expression for the fringe width.
उत्तर
For any other incoherent source of light a steady interference pattern can never be obtained, even if the sources emit waves of equal wavelengths and equal amplitudes. This is because the waves emitted by a source undergo rapid and irregular changes of phase, so that the intensity at any point is never constant. Naturally the phase difference between the waves emitted by the two sources cannot remain constant.
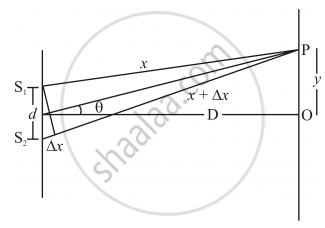
The two waves interfering at P have different distances S1P = x and S2P = x + Δx.
So, for the two sources S1 and S2we can respectively write,
`I_1 = I_(01) sin (kx -wt)`
`I_1 = I_(02) sin (k(x +Deltax)-wt) =I_(02)sin(kx -wt +delta)`
`delta = kDeltax =((2pi)/lambda) xx Delta x`
The resultant can be written as,
`I =I_0sin(kx -wt +epsi)
Where` I_0^2 =I_(01)^2 + I_(02)^2 +2I_(01) I_(02) cos delta`
And tan`epsi = I_(02) sin delta /(I_(01) +I_(02)cos delta)`
The condition for constructive (bright fringe) and destructive (dark fringe) interference are as follows;
δ = 2nπ for bright fringes
δ = (2n + 1) π for dark fringes
Where n is an integer.
Now to find the fringe width,
The path difference is `Deltax =S_2P-S_1P` nearly equal to d `sintheta =d tantheta =(dy)/D`
Hence we can write, `y=(nlambdaD)/d ,n` is an integer.
APPEARS IN
संबंधित प्रश्न
In a double-slit experiment the angular width of a fringe is found to be 0.2° on a screen placed 1 m away. The wavelength of light used is 600 nm. What will be the angular width of the fringe if the entire experimental apparatus is immersed in water? Take refractive index of water to be 4/3.
Write three characteristic features to distinguish between the interference fringes in Young's double slit experiment and the diffraction pattern obtained due to a narrow single slit.
Two transparent slabs having equal thickness but different refractive indices µ1 and µ2are pasted side by side to form a composite slab. This slab is placed just after the double slit in a Young's experiment so that the light from one slit goes through one material and the light from the other slit goes through the other material. What should be the minimum thickness of the slab so that there is a minimum at the point P0 which is equidistant from the slits?
A parallel beam of monochromatic light is used in a Young's double slit experiment. The slits are separated by a distance d and the screen is placed parallel to the plane of the slits. Slow that if the incident beam makes an angle \[\theta = \sin^{- 1} \left( \frac{\lambda}{2d} \right)\] with the normal to the plane of the slits, there will be a dark fringe at the centre P0 of the pattern.
The line-width of a bright fringe is sometimes defined as the separation between the points on the two sides of the central line where the intensity falls to half the maximum. Find the line-width of a bright fringe in a Young's double slit experiment in terms of \[\lambda,\] d and D where the symbols have their usual meanings.
In Young’s double-slit experiment, show that:
`beta = (lambda "D")/"d"` where the terms have their usual meaning.
Draw the intensity distribution as function of phase angle when diffraction of light takes place through coherently illuminated single slit.
The central fringe of the interference pattern produced by the light of wavelength 6000 Å is found to shift to the position of the fourth bright fringe after a glass plate of refractive index 1.5 is introduced in the path of one of the beams. The thickness of the glass plate would be ______.
In Young's double slit experiment, the distance of the 4th bright fringe from the centre of the interference pattern is 1.5 mm. The distance between the slits and the screen is 1.5 m, and the wavelength of light used is 500 nm. Calculate the distance between the two slits.
In Young’s double slit experiment, how is interference pattern affected when the following changes are made:
- Slits are brought closer to each other.
- Screen is moved away from the slits.
- Red coloured light is replaced with blue coloured light.
