Advertisements
Advertisements
प्रश्न
Draw the intensity distribution as function of phase angle when diffraction of light takes place through coherently illuminated single slit.
उत्तर
Intensity distribution as function of phase angle, when diffraction of light takes place through coherently illuminated single slit.
The Intensity pattern on the screen is shown in the given figure.
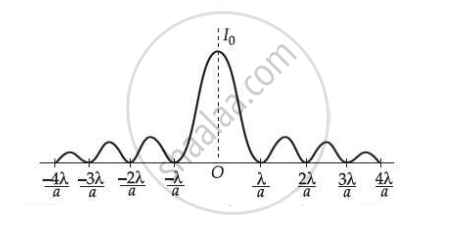
Width of central maximum = `(2"D"λ)/"a"`
APPEARS IN
संबंधित प्रश्न
In young’s double slit experiment, deduce the conditions for obtaining constructive and destructive interference fringes. Hence, deduce the expression for the fringe width.
Show that the fringe pattern on the screen is actually a superposition of slit diffraction from each slit.
In a Young’s double-slit experiment, the slits are separated by 0.28 mm and the screen is placed 1.4 m away. The distance between the central bright fringe and the fourth bright fringe is measured to be 1.2 cm. Determine the wavelength of light used in the experiment.
In Young’s double slit experiment, show graphically how the intensity of light varies with distance
Two coherent sources of light having intensity ratio 81 : 1 produce interference fringes. Calculate the ratio of intensities at the maxima and minima in the interference pattern.
What should be the path difference between two waves reaching a point for obtaining constructive interference in Young’s Double Slit experiment ?
When a beam of light is used to determine the position of an object, the maximum accuracy is achieved, if the light is ______.
An unpolarised beam of intensity 2a2 passes through a thin polaroid. Assuming zero absorption in the polaroid, the intensity of emergent plane polarised light will be
In a Young's double slit experiment, the width of the one of the slit is three times the other slit. The amplitude of the light coming from a slit is proportional to the slit- width. Find the ratio of the maximum to the minimum intensity in the interference pattern.
In an interference experiment, a third bright fringe is obtained at a point on the screen with a light of 700 nm. What should be the wavelength of the light source in order to obtain the fifth bright fringe at the same point?
