Advertisements
Advertisements
प्रश्न
Two coherent sources of light having intensity ratio 81 : 1 produce interference fringes. Calculate the ratio of intensities at the maxima and minima in the interference pattern.
उत्तर
I1 : I2 81:1
If A1 and A2 are the amplitudes of the interfering waves, the ratio of the intensity maximum to the intensity minimum in the fringe system is
`I_max/I_max = ((A_1 +A_2)/(A_1-A_2))^2= ((r+1)/(r-1))^2`
where `r=A_1/A_2` Since the intensity of a wave is directly proportional to the square of its amplitude,
`I_1/I_2=(A_1/A_2)^2=r^2`
`therefore r = sqrt(I_1/I_2)=sqrt81=9`
`therefore I_max/I_max =((9+1)/(9-1))^2=(10/8)^2=(5/4)^2=25/16`
∴ The ratio of the intensities of maxima and minima in the fringe system is 25 : 16.
APPEARS IN
संबंधित प्रश्न
In Young' s experiment the ratio of intensity at the maxima and minima . in the interference pattern is 36 : 16. What is the ratio of the widths of the two slits?
In Young's double slit experiment, plot a graph showing the variation of fringe width versus the distance of the screen from the plane of the slits keeping other parameters same. What information can one obtain from the slope of the curve?
In Young's double slit experiment, describe briefly how bright and dark fringes are obtained on the screen kept in front of a double slit. Hence obtain the expression for the fringe width.
In Young’s double slit experiment, show graphically how the intensity of light varies with distance
In Young's double slit experiment, derive the condition for
(i) constructive interference and
(ii) destructive interference at a point on the screen.
The intensity at the central maxima in Young’s double slit experimental set-up is I0. Show that the intensity at a point where the path difference is λ/3 is I0/4.
How does the fringe width get affected, if the entire experimental apparatus of Young is immersed in water?
Can we perform Young's double slit experiment with sound waves? To get a reasonable "fringe pattern", what should be the order of separation between the slits? How can the bright fringes and the dark fringes be detected in this case?
Suppose white light falls on a double slit but one slit is covered by a violet filter (allowing λ = 400 nm). Describe the nature of the fringe pattern observed.
A thin transparent sheet is placed in front of a Young's double slit. The fringe-width will _____________ .
A Young's double slit experiment is performed with white light.
(a) The central fringe will be white.
(b) There will not be a completely dark fringe.
(c) The fringe next to the central will be red.
(d) The fringe next to the central will be violet.
A plate of thickness t made of a material of refractive index µ is placed in front of one of the slits in a double slit experiment. (a) Find the change in the optical path due to introduction of the plate. (b) What should be the minimum thickness t which will make the intensity at the centre of the fringe pattern zero? Wavelength of the light used is \[\lambda.\] Neglect any absorption of light in the plate.
A double slit S1 − S2 is illuminated by a coherent light of wavelength \[\lambda.\] The slits are separated by a distance d. A plane mirror is placed in front of the double slit at a distance D1 from it and a screen ∑ is placed behind the double slit at a distance D2 from it (see the following figure). The screen ∑ receives only the light reflected by the mirror. Find the fringe-width of the interference pattern on the screen.
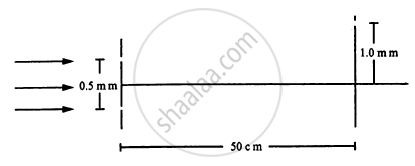
White coherent light (400 nm-700 nm) is sent through the slits of a Young's double slit experiment (see the following figure). The separation between the slits is 0⋅5 mm and the screen is 50 cm away from the slits. There is a hole in the screen at a point 1⋅0 mm away (along the width of the fringes) from the central line. (a) Which wavelength(s) will be absent in the light coming from the hole? (b) Which wavelength(s) will have a strong intensity?
What should be the path difference between two waves reaching a point for obtaining constructive interference in Young’s Double Slit experiment ?
Two slits in Young's interference experiment have width in the ratio 1 : 2. The ratio of intensity at the maxima and minima in their interference is ______.
A thin circular ring of mass M and radius R is rotating about its axis with a constant angular velocity ω. Two objects each of mass m are attached gently to the opposite ends of diameter of the ring. The ring will now rotate with an angular velocity:
The force required to double the length of a steel wire of area 1 cm2, if its Young's modulus Y= 2 × 1011/m2 is:
An unpolarised beam of intensity 2a2 passes through a thin polaroid. Assuming zero absorption in the polaroid, the intensity of emergent plane polarised light will be
Two balls are projected at an angle θ and (90° − θ) to the horizontal with the same speed. The ratio of their maximum vertical heights is:
A slit of width 0.6 mm is illuminated by a beam of light consisting of two wavelengths 600 nm and 480 nm. The diffraction pattern is observed on a screen 1.0 m from the slit. Find:
- The distance of the second bright fringe from the central maximum pertaining to the light of 600 nm.
- The least distance from the central maximum at which bright fringes due to both wavelengths coincide.
In Young's double slit experiment using light of wavelength 600 nm, the slit separation is 0.8 mm and the screen is kept 1.6 m from the plane of the slits. Calculate
- the fringe width
- the distance of (a) third minimum and (b) fifth maximum, from the central maximum.
In Young's double slit experiment the two slits are 0.6 mm distance apart. Interference pattern is observed on a screen at a distance 80 cm from the slits. The first dark fringe is observed on the screen directly opposite to one of the slits. The wavelength of light will be ______ nm.
In Young's double-slit experiment, the separation between the two slits is d and the distance of the screen from the slits is 1000 d. If the first minima fall at a distance d from the central maximum, obtain the relation between d and λ.
In Young's double-slit experiment, the screen is moved away from the plane of the slits. What will be its effect on the following?
- The angular separation of the fringes.
- Fringe-width.
In Young's double slit experiment, show that:
`β = (λ"D")/"d"`
Where the terms have their usual meaning.
