Advertisements
Advertisements
प्रश्न
A slit of width 0.6 mm is illuminated by a beam of light consisting of two wavelengths 600 nm and 480 nm. The diffraction pattern is observed on a screen 1.0 m from the slit. Find:
- The distance of the second bright fringe from the central maximum pertaining to the light of 600 nm.
- The least distance from the central maximum at which bright fringes due to both wavelengths coincide.
उत्तर
(i) Distance of 2nd bright fringe from central maximum = `(2λ"D")/"d"`
= `(2 xx 600 xx 10^-19 xx 1)/(0.6 xx 10^-3)`
= 20 × 10−4 m
(ii) If nth bright fringe due to 600 nm coincides with (n + 1)th bright fringe due to 480 nm, then
`("n"λ_1"D")/"d" = (("n" - 1)λ_2"D")/"d"`
Or, nλ1D = (n + 1)λ2D
Or, `"n"/(("n" - 1)) = λ_2/λ_1`
Or, `"n"/(("n" - 1)) = 600/480`
`"n" xx 480 = 600 ("n" - 1)`
`480 "n" = 600 "n" - 600`
600 = `600 "n" - 480 "n"`
600 = `600 "n" - 480 "n"`
600 = `120 "n"`
∴ n = `600/120`
n = 5
So, the least distance from the central maximum = `(5 xx 480 xx 10^-9 xx 1)/(0.6 xx 10^-3)`
= 4 × 10−3 m
= 4 mm
APPEARS IN
संबंधित प्रश्न
In Young's double slit experiment, describe briefly how bright and dark fringes are obtained on the screen kept in front of a double slit. Hence obtain the expression for the fringe width.
How does the fringe width get affected, if the entire experimental apparatus of Young is immersed in water?
If the source of light used in a Young's double slit experiment is changed from red to violet, ___________ .
A Young's double slit apparatus has slits separated by 0⋅28 mm and a screen 48 cm away from the slits. The whole apparatus is immersed in water and the slits are illuminated by red light \[\left( \lambda = 700\text{ nm in vacuum} \right).\] Find the fringe-width of the pattern formed on the screen.
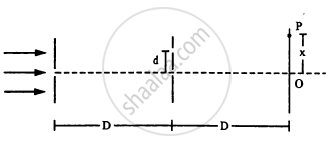
Consider the arrangement shown in the figure. The distance D is large compared to the separation d between the slits.
- Find the minimum value of d so that there is a dark fringe at O.
- Suppose d has this value. Find the distance x at which the next bright fringe is formed.
- Find the fringe-width.
In Young’s double slit experiment, what is the effect on fringe pattern if the slits are brought closer to each other?
A projectile can have the same range R for two angles of projection. If t1 and t2 be the times of flight in two cases, then what is the product of two times of flight?
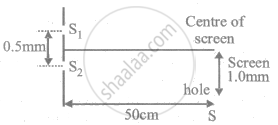
In Young's double slit experiment shown in figure S1 and S2 are coherent sources and S is the screen having a hole at a point 1.0 mm away from the central line. White light (400 to 700 nm) is sent through the slits. Which wavelength passing through the hole has strong intensity?
In a Young’s double slit experiment, the path difference at a certain point on the screen between two interfering waves is `1/8`th of the wavelength. The ratio of intensity at this point to that at the centre of a bright fringe is close to ______.
Interference fringes are observed on a screen by illuminating two thin slits 1 mm apart with a light source (λ = 632.8 nm). The distance between the screen and the slits is 100 cm. If a bright fringe is observed on a screen at distance of 1.27 mm from the central bright fringe, then the path difference between the waves, which are reaching this point from the slits is close to :
