Advertisements
Advertisements
प्रश्न
In Young's double slit experiment, describe briefly how bright and dark fringes are obtained on the screen kept in front of a double slit. Hence obtain the expression for the fringe width.
उत्तर
In Young's double-slit experiment, the wavefronts from the two illuminated slits superpose on the screen. This leads to formation of alternate dark and bright fringes due to constructive and destructive interference, respectively. At the centre C of the screen, the intensity of light is maximum and it is called central maxima.
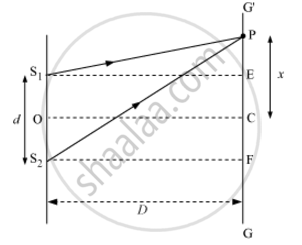
Let S1 and S2 be two slits separated by a distance d. GG'is the screen at a distance D from the slits S1 and S2. Point C is equidistant from both the slits. The intensity of light will be maximum at this point because the path difference of the waves reaching this point will be zero.
At point P, the path difference between the rays coming from the slits S1 and S2 is S2P - S1P.
Now, S1 S2 = d, EF = d, and S2F= D
∴In ΔS2PF,
`S_2P=[S_2F^2+PF^2]^(1/2)`
`S_2P=[D^2+(x+d/2)^2]^(1/2)`
`=D[1+(x+d/2)/D^2]^(1/2)`
Similarly, in ΔS1PE,
`S_1P=D[1+(x-d/2)^2/D^2]^(1/2)`
`:.S_2P-S_1P=D[1+1/2(x+d/2)^2/D^2]-D[1+1/2(x-d/2)^2/D^2]`
On expanding it binomially,
`S_2P-S_1P=1/(2D)[4xd/2]=(xd)/D`
For bright fringes (constructive interference), the path difference is an integral multiple of wavelengths, i.e. path difference is nλ.
`:.nlambda=(xd)/D`
`x=(nlambdaD)/d`where n = 0, 1, 2, 3, 4, …
For n = 0, x0 = 0
n =1, `x_1=(lambdaD)d`
n = 2, `x_2=(2lambdaD)/d`
n =3, `x_3=(3lambdaD)d`
`n=n, x_n = (nlambdaD)/d`
Fringe width (β) → Separation between the centres of two consecutive bright fringes is called the width of a dark fringe.
`:.beta_1=x_n-x_(n-1)=(lambdaD)/d`
Similarly, for dark fringes,
`x_n=(2n-1)lambda/2D/d`
For n =1, `x_1=(lambdaD)/(2d)`
For n =2, `x_2=(3lambdaD)/(2d)`
The separation between the centres of two consecutive dark interference fringes is the width of a bright fringe.
`:. beta_2=x_n-x_(n-1)=(lambdaD)/d`
∴β1 = β2
All the bright and dark fringes are of equal width as β1 = β2
APPEARS IN
संबंधित प्रश्न
What is the effect on the fringe width if the distance between the slits is reduced keeping other parameters same?
Show that the angular width of the first diffraction fringe is half that of the central fringe.
In Young's double slit experiment, using monochromatic light of wavelength λ, the intensity of light at a point on the screen where path difference is λ, is K units. Find out the intensity of light at a point where path difference is `λ/3`.
In a Young’s double-slit experiment, the slits are separated by 0.28 mm and the screen is placed 1.4 m away. The distance between the central bright fringe and the fourth bright fringe is measured to be 1.2 cm. Determine the wavelength of light used in the experiment.
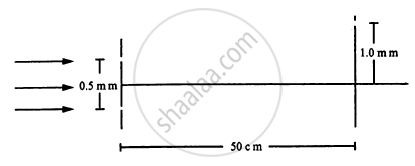
White coherent light (400 nm-700 nm) is sent through the slits of a Young's double slit experiment (see the following figure). The separation between the slits is 0⋅5 mm and the screen is 50 cm away from the slits. There is a hole in the screen at a point 1⋅0 mm away (along the width of the fringes) from the central line. (a) Which wavelength(s) will be absent in the light coming from the hole? (b) Which wavelength(s) will have a strong intensity?
In Young’s double-slit experiment, using monochromatic light, fringes are obtained on a screen placed at some distance from the slits. If the screen is moved by 5 x 10-2 m towards the slits, the change in the fringe width is 3 x 10-5 m. If the distance between the two slits is 10-3 m, calculate the wavelength of the light used.
A projectile can have the same range R for two angles of projection. If t1 and t2 be the times of flight in two cases, then what is the product of two times of flight?
Consider a two-slit interference arrangement (Figure) such that the distance of the screen from the slits is half the distance between the slits. Obtain the value of D in terms of λ such that the first minima on the screen falls at a distance D from the centre O.
In Young's double slit experiment the two slits are 0.6 mm distance apart. Interference pattern is observed on a screen at a distance 80 cm from the slits. The first dark fringe is observed on the screen directly opposite to one of the slits. The wavelength of light will be ______ nm.
In Young’s double slit experiment, how is interference pattern affected when the following changes are made:
- Slits are brought closer to each other.
- Screen is moved away from the slits.
- Red coloured light is replaced with blue coloured light.
