Advertisements
Advertisements
प्रश्न
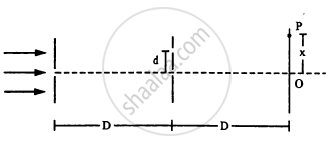
Consider the arrangement shown in the figure. The distance D is large compared to the separation d between the slits.
- Find the minimum value of d so that there is a dark fringe at O.
- Suppose d has this value. Find the distance x at which the next bright fringe is formed.
- Find the fringe-width.
उत्तर
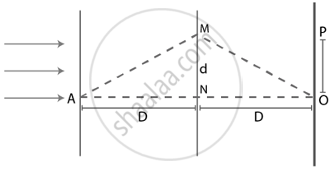
From the figure,
Δx = AMO − ANO
Here AM = MO = √[D2 + d2] AND AN = NO = D
=> Δx = 2(AM − AN) = 2 {√[D2 + d2] - D}
For minima at O,
2 {√[D2 + d2] − D} = (n +(1/2)) λ
Solving above equation for d, we get
d = √[Dλ/2]
(b) width of the dark fringe = w = Dλ/d
Now, the location x is given by
x = Dλ/[2√(Dλ/2)]
=> x = d
(c) As x = w/2
=> w = 2x = 2d
APPEARS IN
संबंधित प्रश्न
(i) In Young's double-slit experiment, deduce the condition for (a) constructive and (b) destructive interferences at a point on the screen. Draw a graph showing variation of intensity in the interference pattern against position 'x' on the screen.
(b) Compare the interference pattern observed in Young's double-slit experiment with single-slit diffraction pattern, pointing out three distinguishing features.
Show that the angular width of the first diffraction fringe is half that of the central fringe.
In a double-slit experiment the angular width of a fringe is found to be 0.2° on a screen placed 1 m away. The wavelength of light used is 600 nm. What will be the angular width of the fringe if the entire experimental apparatus is immersed in water? Take refractive index of water to be 4/3.
What is the effect on the interference fringes to a Young’s double slit experiment when
(i) the separation between the two slits is decreased?
(ii) the width of a source slit is increased?
(iii) the monochromatic source is replaced by a source of white light?
Justify your answer in each case.
Can we perform Young's double slit experiment with sound waves? To get a reasonable "fringe pattern", what should be the order of separation between the slits? How can the bright fringes and the dark fringes be detected in this case?
A thin transparent sheet is placed in front of a Young's double slit. The fringe-width will _____________ .
If Young's double slit experiment is performed in water, _________________ .
Find the angular separation between the consecutive bright fringes in a Young's double slit experiment with blue-green light of wavelength 500 nm. The separation between the slits is \[2 \cdot 0 \times {10}^{- 3}m.\]
White light is used in a Young's double slit experiment. Find the minimum order of the violet fringe \[\left( \lambda = 400\text{ nm} \right)\] which overlaps with a red fringe \[\left( \lambda = 700\text{ nm} \right).\]
A transparent paper (refractive index = 1.45) of thickness 0.02 mm is pasted on one of the slits of a Young's double slit experiment which uses monochromatic light of wavelength 620 nm. How many fringes will cross through the centre if the paper is removed?
A thin paper of thickness 0.02 mm having a refractive index 1.45 is pasted across one of the slits in a Young's double slit experiment. The paper transmits 4/9 of the light energy falling on it. (a) Find the ratio of the maximum intensity to the minimum intensity in the fringe pattern. (b) How many fringes will cross through the centre if an identical paper piece is pasted on the other slit also? The wavelength of the light used is 600 nm.
How is the fringe width of an interference pattern in Young's double-slit experiment affected if the two slits are brought closer to each other?
How will the interference pattern in Young's double-slit experiment be affected if the phase difference between the light waves emanating from the two slits S1 and S2 changes from 0 to π and remains constant?
In a double-slit experiment with monochromatic light, fringes are obtained on a screen placed at some distance from the plane of slits. If the screen is moved by 5 × 10-2 m towards the slits, the change in fringe width is 3 × 10-3 cm. If the distance between the slits is 1 mm, then the wavelength of the light will be ______ nm.
A fringe width of 6 mm was produced for two slits separated by 1 mm apart. The screen is placed 10 m away. The wavelength of light used is 'x' nm. The value of 'x' to the nearest integer is ______.
Monochromatic green light of wavelength 5 × 10-7 m illuminates a pair of slits 1 mm apart. The separation of bright lines in the interference pattern formed on a screen 2 m away is ______.
- Assertion (A): In Young's double slit experiment all fringes are of equal width.
- Reason (R): The fringe width depends upon the wavelength of light (λ) used, the distance of the screen from the plane of slits (D) and slits separation (d).
In Young's double slit experiment, show that:
`β = (λ"D")/"d"`
Where the terms have their usual meaning.
In Young’s double slit experiment, how is interference pattern affected when the following changes are made:
- Slits are brought closer to each other.
- Screen is moved away from the slits.
- Red coloured light is replaced with blue coloured light.
