Advertisements
Advertisements
प्रश्न
In Young's double slit experiment, show that:
`β = (λ"D")/"d"`
Where the terms have their usual meaning.
उत्तर
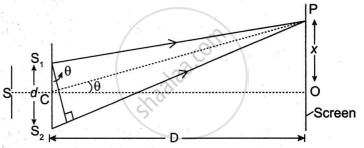
Assume that S is a light source that is receiving light from another light source. Two line sources, S1 and S2, are equally spaced apart from light source S.
Let S1S2 = d
Path difference between waves at point P,
S2P - S1P = S2A
ΔS1S2A and ΔPCO are similar to each other.
∴ `("S"_2"A")/("S"_1"S"_2) =("OP")/("CP")`
Since CO is very much greater than S1S2,
So CP ≈ CO
∴ `("S"_2"A")/("S"_1"S"_2) = ("OP")/("CO")`
`("S"_2"A")/"d" = x/"D"`
∴ Path difference = `x/"D"`
For bright fringes, = mλ
`x = m ("D"λ)/"d"`
For mth and (m + 1)th fringe,
`x_m = m ("D"λ)/"d"` and
`x_(m + 1) = (m + 1) ("D"λ)/"d"`
Fringe width, `β = x_(m + 1) - x_m`
= `(m + 1) ("D"λ)/"d" - m ("D"λ)/"d"`
`β = ("D"λ)/"d"`
APPEARS IN
संबंधित प्रश्न
(i) In Young's double-slit experiment, deduce the condition for (a) constructive and (b) destructive interferences at a point on the screen. Draw a graph showing variation of intensity in the interference pattern against position 'x' on the screen.
(b) Compare the interference pattern observed in Young's double-slit experiment with single-slit diffraction pattern, pointing out three distinguishing features.
In Young’s experiment, the ratio of intensity at the maxima and minima in an interference
pattern is 36 : 9. What will be the ratio of the intensities of two interfering waves?
A mica strip and a polystyrene strip are fitted on the two slits of a double slit apparatus. The thickness of the strips is 0.50 mm and the separation between the slits is 0.12 cm. The refractive index of mica and polystyrene are 1.58 and 1.55, respectively, for the light of wavelength 590 nm which is used in the experiment. The interference is observed on a screen at a distance one metre away. (a) What would be the fringe-width? (b) At what distance from the centre will the first maximum be located?
In Young’s double-slit experiment, using monochromatic light, fringes are obtained on a screen placed at some distance from the slits. If the screen is moved by 5 x 10-2 m towards the slits, the change in the fringe width is 3 x 10-5 m. If the distance between the two slits is 10-3 m, calculate the wavelength of the light used.
Answer the following question.
Write the conditions on path difference under which (i) constructive (ii) destructive interference occur in Young's double-slit experiment.
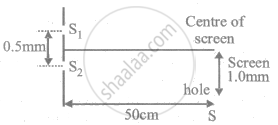
In Young's double slit experiment shown in figure S1 and S2 are coherent sources and S is the screen having a hole at a point 1.0 mm away from the central line. White light (400 to 700 nm) is sent through the slits. Which wavelength passing through the hole has strong intensity?
In a Young’s double slit experiment, the path difference at a certain point on the screen between two interfering waves is `1/8`th of the wavelength. The ratio of intensity at this point to that at the centre of a bright fringe is close to ______.
Using Young’s double slit experiment, a monochromatic light of wavelength 5000Å produces fringes of fringe width 0.5 mm. If another monochromatic light of wavelength 6000Å is used and the separation between the slits is doubled, then the new fringe width will be ______.
The central fringe of the interference pattern produced by the light of wavelength 6000 Å is found to shift to the position of the fourth bright fringe after a glass plate of refractive index 1.5 is introduced in the path of one of the beams. The thickness of the glass plate would be ______.
In Young’s double slit experiment, how is interference pattern affected when the following changes are made:
- Slits are brought closer to each other.
- Screen is moved away from the slits.
- Red coloured light is replaced with blue coloured light.
