Advertisements
Advertisements
Question
In Young's double slit experiment, show that:
`β = (λ"D")/"d"`
Where the terms have their usual meaning.
Solution
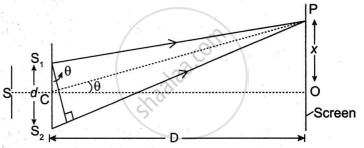
Assume that S is a light source that is receiving light from another light source. Two line sources, S1 and S2, are equally spaced apart from light source S.
Let S1S2 = d
Path difference between waves at point P,
S2P - S1P = S2A
ΔS1S2A and ΔPCO are similar to each other.
∴ `("S"_2"A")/("S"_1"S"_2) =("OP")/("CP")`
Since CO is very much greater than S1S2,
So CP ≈ CO
∴ `("S"_2"A")/("S"_1"S"_2) = ("OP")/("CO")`
`("S"_2"A")/"d" = x/"D"`
∴ Path difference = `x/"D"`
For bright fringes, = mλ
`x = m ("D"λ)/"d"`
For mth and (m + 1)th fringe,
`x_m = m ("D"λ)/"d"` and
`x_(m + 1) = (m + 1) ("D"λ)/"d"`
Fringe width, `β = x_(m + 1) - x_m`
= `(m + 1) ("D"λ)/"d" - m ("D"λ)/"d"`
`β = ("D"λ)/"d"`
APPEARS IN
RELATED QUESTIONS
The ratio of the intensities at minima to the maxima in the Young's double slit experiment is 9 : 25. Find the ratio of the widths of the two slits.
In Young’s experiment, the ratio of intensity at the maxima and minima in an interference
pattern is 36 : 9. What will be the ratio of the intensities of two interfering waves?
How does an unpolarized light incident on a polaroid get polarized? Describe briefly, with the help of a necessary diagram, the polarization of light by reflection from a transparent medium.
A source emitting light of wavelengths 480 nm and 600 nm is used in a double-slit interference experiment. The separation between the slits is 0.25 mm and the interference is observed on a screen placed at 150 cm from the slits. Find the linear separation between the first maximum (next to the central maximum) corresponding to the two wavelengths.
A double slit S1 − S2 is illuminated by a coherent light of wavelength \[\lambda.\] The slits are separated by a distance d. A plane mirror is placed in front of the double slit at a distance D1 from it and a screen ∑ is placed behind the double slit at a distance D2 from it (see the following figure). The screen ∑ receives only the light reflected by the mirror. Find the fringe-width of the interference pattern on the screen.
Draw the intensity distribution as function of phase angle when diffraction of light takes place through coherently illuminated single slit.
A thin circular ring of mass M and radius R is rotating about its axis with a constant angular velocity ω. Two objects each of mass m are attached gently to the opposite ends of diameter of the ring. The ring will now rotate with an angular velocity:
The Young's double slit experiment is performed with blue and with green light of wavelengths 4360Å and 5460Å respectively. If x is the distance of 4th maxima from the central one, then:
ASSERTION (A): In an interference pattern observed in Young's double slit experiment, if the separation (d) between coherent sources as well as the distance (D) of the screen from the coherent sources both are reduced to 1/3rd, then new fringe width remains the same.
REASON (R): Fringe width is proportional to (d/D).
How will the interference pattern in Young's double-slit experiment be affected if the phase difference between the light waves emanating from the two slits S1 and S2 changes from 0 to π and remains constant?
