Advertisements
Advertisements
Question
A double slit S1 − S2 is illuminated by a coherent light of wavelength \[\lambda.\] The slits are separated by a distance d. A plane mirror is placed in front of the double slit at a distance D1 from it and a screen ∑ is placed behind the double slit at a distance D2 from it (see the following figure). The screen ∑ receives only the light reflected by the mirror. Find the fringe-width of the interference pattern on the screen.
Solution
Given:-
Separation between the two slits = d
Wavelength of the coherent light =λ
Distance between the slit and mirror is D1.
Distance between the slit and screen is D2.
Therefore,
apparent distance of the screen from the slits,
\[D = 2 D_1 + D_2 \]
Fringe width, \[\beta = \frac{\lambda D}{d} = \frac{\left( 2 D_1 + D_2 \right) \lambda}{d}\]
Hence, the required fringe width is \[\frac{\left( 2 D_1 + D_2 \right) \lambda}{d}.\]
APPEARS IN
RELATED QUESTIONS
(i) In Young's double-slit experiment, deduce the condition for (a) constructive and (b) destructive interferences at a point on the screen. Draw a graph showing variation of intensity in the interference pattern against position 'x' on the screen.
(b) Compare the interference pattern observed in Young's double-slit experiment with single-slit diffraction pattern, pointing out three distinguishing features.
In Young's double slit experiment, plot a graph showing the variation of fringe width versus the distance of the screen from the plane of the slits keeping other parameters same. What information can one obtain from the slope of the curve?
In Young's double slit experiment, describe briefly how bright and dark fringes are obtained on the screen kept in front of a double slit. Hence obtain the expression for the fringe width.
A beam of light consisting of two wavelengths, 650 nm and 520 nm, is used to obtain interference fringes in a Young’s double-slit experiment.
Find the distance of the third bright fringe on the screen from the central maximum for wavelength 650 nm.
A beam of light consisting of two wavelengths, 650 nm and 520 nm, is used to obtain interference fringes in a Young’s double-slit experiment.
What is the least distance from the central maximum where the bright fringes due to both the wavelengths coincide?
Using analytical method for interference bands, obtain an expression for path difference between two light waves.
Explain two features to distinguish between the interference pattern in Young's double slit experiment with the diffraction pattern obtained due to a single slit.
How does an unpolarized light incident on a polaroid get polarized? Describe briefly, with the help of a necessary diagram, the polarization of light by reflection from a transparent medium.
Two coherent sources of light having intensity ratio 81 : 1 produce interference fringes. Calculate the ratio of intensities at the maxima and minima in the interference pattern.
In a double slit interference experiment, the separation between the slits is 1.0 mm, the wavelength of light used is 5.0 × 10−7 m and the distance of the screen from the slits is 1.0m. (a) Find the distance of the centre of the first minimum from the centre of the central maximum. (b) How many bright fringes are formed in one centimetre width on the screen?
A plate of thickness t made of a material of refractive index µ is placed in front of one of the slits in a double slit experiment. (a) Find the change in the optical path due to introduction of the plate. (b) What should be the minimum thickness t which will make the intensity at the centre of the fringe pattern zero? Wavelength of the light used is \[\lambda.\] Neglect any absorption of light in the plate.
In a Young's double slit experiment, using monochromatic light, the fringe pattern shifts by a certain distance on the screen when a mica sheet of refractive index 1.6 and thickness 1.964 micron (1 micron = 10−6 m) is introduced in the path of one of the interfering waves. The mica sheet is then removed and the distance between the screen and the slits is doubled. It is found that the distance between the successive maxima now is the same as the observed fringe-shift upon the introduction of the mica sheet. Calculate the wavelength of the monochromatic light used in the experiment.
Consider the arrangement shown in the figure. By some mechanism, the separation between the slits S3 and S4 can be changed. The intensity is measured at the point P, which is at the common perpendicular bisector of S1S2 and S2S4. When \[z = \frac{D\lambda}{2d},\] the intensity measured at P is I. Find the intensity when z is equal to

(a) \[\frac{D\lambda}{d}\]
(b) \[\frac{3D\lambda}{2d}\] and
(c) \[\frac{2D\lambda}{d}\]
What should be the path difference between two waves reaching a point for obtaining constructive interference in Young’s Double Slit experiment ?
In Young's double slit experiment the slits are 0.589 mm apart and the interference is observed on a screen placed at a distance of 100 cm from the slits. It is found that the 9th bright fringe is at a distance of 7.5 mm from the dark fringe which is second from the center of the fringe pattern. Find the wavelength of the light used.
Draw the intensity distribution as function of phase angle when diffraction of light takes place through coherently illuminated single slit.
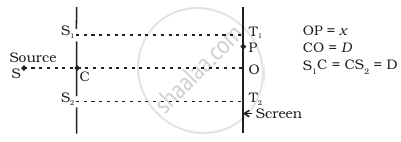
Consider a two-slit interference arrangement (Figure) such that the distance of the screen from the slits is half the distance between the slits. Obtain the value of D in terms of λ such that the first minima on the screen falls at a distance D from the centre O.
In Young's double slit experiment using light of wavelength 600 nm, the slit separation is 0.8 mm and the screen is kept 1.6 m from the plane of the slits. Calculate
- the fringe width
- the distance of (a) third minimum and (b) fifth maximum, from the central maximum.
Two beams of light having intensities I and 41 interfere to produce a fringe pattern on a screen. The phase difference between the two beams are π/2 and π/3 at points A and B respectively. The difference between the resultant intensities at the two points is xl. The value of x will be ______.
In Young’s double slit experiment, how is interference pattern affected when the following changes are made:
- Slits are brought closer to each other.
- Screen is moved away from the slits.
- Red coloured light is replaced with blue coloured light.
