Advertisements
Advertisements
Question
White coherent light (400 nm-700 nm) is sent through the slits of a Young's double slit experiment (see the following figure). The separation between the slits is 0⋅5 mm and the screen is 50 cm away from the slits. There is a hole in the screen at a point 1⋅0 mm away (along the width of the fringes) from the central line. (a) Which wavelength(s) will be absent in the light coming from the hole? (b) Which wavelength(s) will have a strong intensity?
Advertisements
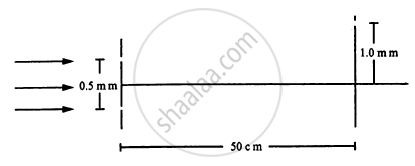
Solution
Given:-
Separation between two slits,
\[d = 0 . 5 mm = 0 . 5 \times {10}^{- 3} m\]
Wavelength of the light,
\[\lambda = 400\text{ nm to 700 nm}\]
Distance of the screen from the slit,
\[D = 50 cm = 0 . 5 m\]
Position of hole on the screen,
\[y_n = 1 mm = 1 \times {10}^{- 3} m\]
(a) The wavelength(s) will be absent in the light coming from the hole, which will form a dark fringe at the position of hole.
\[y_n = \frac{\left( 2n + 1 \right) \lambda_n}{2}\frac{D}{d}\text{, where n = 0, 1, 2, ......}\]
\[\Rightarrow \lambda_n = \frac{2}{\left( 2n + 1 \right)} \frac{y_n d}{D}\]
\[= \frac{2}{\left( 2n + 1 \right)} \times \frac{{10}^{- 3} \times 0 . 05 \times {10}^{- 3}}{0 . 5}\]
\[= \frac{2}{\left( 2n + 1 \right)} \times {10}^{- 6} m\]
\[= \frac{2}{\left( 2n + 1 \right)} \times {10}^3 nm\]
For n = 1,
\[ \lambda_1 = \left( \frac{2}{3} \right) \times 1000 = 667 nm\]
For n = 2,
\[ \lambda_2 = \left( \frac{2}{5} \right) \times 1000 = 400 nm\]
Thus, the light waves of wavelength 400 nm and 667 nm will be absent from the light coming from the hole.
(b) The wavelength(s) will have a strong intensity, which will form a bright fringe at the position of the hole.
So, \[y_n = n \lambda_n \frac{D}{d}\]
\[ \Rightarrow \lambda_n = y_n \frac{d}{nD}\]
For n = 1,
\[ \lambda_1 = y_n \frac{d}{D}\]
\[ = {10}^{- 3} \times \left( 0 . 5 \right) \times \frac{{10}^{- 3}}{0 . 5}\]
\[ = {10}^{- 6} m = 1000 nm.\]
But 1000 nm does not fall in the range 400 nm to 700 nm.
Again, for n = 2,
\[ \lambda_2 = y_n \frac{d}{2D} = 500 nm\]
So, the light of wavelength 500 nm will have strong intensity.
APPEARS IN
RELATED QUESTIONS
What is the effect on the fringe width if the distance between the slits is reduced keeping other parameters same?
The ratio of the intensities at minima to the maxima in the Young's double slit experiment is 9 : 25. Find the ratio of the widths of the two slits.
In Young's double slit experiment, derive the condition for
(i) constructive interference and
(ii) destructive interference at a point on the screen.
Two polaroids ‘A’ and ‘B’ are kept in crossed position. How should a third polaroid ‘C’ be placed between them so that the intensity of polarized light transmitted by polaroid B reduces to 1/8th of the intensity of unpolarized light incident on A?
In Young’s experiment interference bands were produced on a screen placed at 150 cm from two slits, 0.15 mm apart and illuminated by the light of wavelength 6500 Å. Calculate the fringe width.
Suppose white light falls on a double slit but one slit is covered by a violet filter (allowing λ = 400 nm). Describe the nature of the fringe pattern observed.
Find the angular separation between the consecutive bright fringes in a Young's double slit experiment with blue-green light of wavelength 500 nm. The separation between the slits is \[2 \cdot 0 \times {10}^{- 3}m.\]
In a Young's double slit experiment, using monochromatic light, the fringe pattern shifts by a certain distance on the screen when a mica sheet of refractive index 1.6 and thickness 1.964 micron (1 micron = 10−6 m) is introduced in the path of one of the interfering waves. The mica sheet is then removed and the distance between the screen and the slits is doubled. It is found that the distance between the successive maxima now is the same as the observed fringe-shift upon the introduction of the mica sheet. Calculate the wavelength of the monochromatic light used in the experiment.
Two transparent slabs having equal thickness but different refractive indices µ1 and µ2are pasted side by side to form a composite slab. This slab is placed just after the double slit in a Young's experiment so that the light from one slit goes through one material and the light from the other slit goes through the other material. What should be the minimum thickness of the slab so that there is a minimum at the point P0 which is equidistant from the slits?
In a Young's double slit interference experiment, the fringe pattern is observed on a screen placed at a distance D from the slits. The slits are separated by a distance d and are illuminated by monochromatic light of wavelength \[\lambda.\] Find the distance from the central point where the intensity falls to (a) half the maximum, (b) one-fourth the maximum.
Consider the arrangement shown in the figure. By some mechanism, the separation between the slits S3 and S4 can be changed. The intensity is measured at the point P, which is at the common perpendicular bisector of S1S2 and S2S4. When \[z = \frac{D\lambda}{2d},\] the intensity measured at P is I. Find the intensity when z is equal to
(a) \[\frac{D\lambda}{d}\]
(b) \[\frac{3D\lambda}{2d}\] and
(c) \[\frac{2D\lambda}{d}\]
A projectile can have the same range R for two angles of projection. If t1 and t2 be the times of flight in two cases, then what is the product of two times of flight?
Two slits, 4mm apart, are illuminated by light of wavelength 6000 A° what will be the fringe width on a screen placed 2 m from the slits?
Why is the diffraction of sound waves more evident in daily experience than that of light wave?
In a Young’s double slit experiment, the path difference at a certain point on the screen between two interfering waves is `1/8`th of the wavelength. The ratio of intensity at this point to that at the centre of a bright fringe is close to ______.
How will the interference pattern in Young's double-slit experiment be affected if the source slit is moved away from the plane of the slits?
In a Young's double slit experiment, the width of the one of the slit is three times the other slit. The amplitude of the light coming from a slit is proportional to the slit- width. Find the ratio of the maximum to the minimum intensity in the interference pattern.
A fringe width of 6 mm was produced for two slits separated by 1 mm apart. The screen is placed 10 m away. The wavelength of light used is 'x' nm. The value of 'x' to the nearest integer is ______.
The central fringe of the interference pattern produced by the light of wavelength 6000 Å is found to shift to the position of the fourth bright fringe after a glass plate of refractive index 1.5 is introduced in the path of one of the beams. The thickness of the glass plate would be ______.
In Young’s double slit experiment, how is interference pattern affected when the following changes are made:
- Slits are brought closer to each other.
- Screen is moved away from the slits.
- Red coloured light is replaced with blue coloured light.
