Advertisements
Advertisements
Question
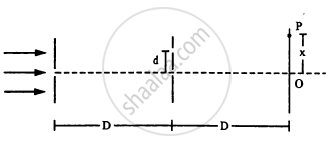
Consider the arrangement shown in the figure. The distance D is large compared to the separation d between the slits.
- Find the minimum value of d so that there is a dark fringe at O.
- Suppose d has this value. Find the distance x at which the next bright fringe is formed.
- Find the fringe-width.
Solution
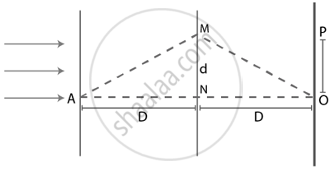
From the figure,
Δx = AMO − ANO
Here AM = MO = √[D2 + d2] AND AN = NO = D
=> Δx = 2(AM − AN) = 2 {√[D2 + d2] - D}
For minima at O,
2 {√[D2 + d2] − D} = (n +(1/2)) λ
Solving above equation for d, we get
d = √[Dλ/2]
(b) width of the dark fringe = w = Dλ/d
Now, the location x is given by
x = Dλ/[2√(Dλ/2)]
=> x = d
(c) As x = w/2
=> w = 2x = 2d
APPEARS IN
RELATED QUESTIONS
Show that the fringe pattern on the screen is actually a superposition of slit diffraction from each slit.
What is the effect on the fringe width if the distance between the slits is reduced keeping other parameters same?
The ratio of the intensities at minima to the maxima in the Young's double slit experiment is 9 : 25. Find the ratio of the widths of the two slits.
Explain two features to distinguish between the interference pattern in Young's double slit experiment with the diffraction pattern obtained due to a single slit.
A monochromatic light of wavelength 500 nm is incident normally on a single slit of width 0.2 mm to produce a diffraction pattern. Find the angular width of the central maximum obtained on the screen.
Estimate the number of fringes obtained in Young's double slit experiment with fringe width 0.5 mm, which can be accommodated within the region of total angular spread of the central maximum due to single slit.
In Young’s double slit experiment, show graphically how the intensity of light varies with distance
How does an unpolarized light incident on a polaroid get polarized? Describe briefly, with the help of a necessary diagram, the polarization of light by reflection from a transparent medium.
How does the fringe width get affected, if the entire experimental apparatus of Young is immersed in water?
A mica strip and a polystyrene strip are fitted on the two slits of a double slit apparatus. The thickness of the strips is 0.50 mm and the separation between the slits is 0.12 cm. The refractive index of mica and polystyrene are 1.58 and 1.55, respectively, for the light of wavelength 590 nm which is used in the experiment. The interference is observed on a screen at a distance one metre away. (a) What would be the fringe-width? (b) At what distance from the centre will the first maximum be located?
A thin paper of thickness 0.02 mm having a refractive index 1.45 is pasted across one of the slits in a Young's double slit experiment. The paper transmits 4/9 of the light energy falling on it. (a) Find the ratio of the maximum intensity to the minimum intensity in the fringe pattern. (b) How many fringes will cross through the centre if an identical paper piece is pasted on the other slit also? The wavelength of the light used is 600 nm.
A parallel beam of monochromatic light is used in a Young's double slit experiment. The slits are separated by a distance d and the screen is placed parallel to the plane of the slits. Slow that if the incident beam makes an angle \[\theta = \sin^{- 1} \left( \frac{\lambda}{2d} \right)\] with the normal to the plane of the slits, there will be a dark fringe at the centre P0 of the pattern.
Draw the intensity distribution as function of phase angle when diffraction of light takes place through coherently illuminated single slit.
In Young's double slit experiment, the minimum amplitude is obtained when the phase difference of super-imposing waves is: (where n = 1, 2, 3, ...)
In a Young’s double slit experiment, the source is white light. One of the holes is covered by a red filter and another by a blue filter. In this case ______.
In a double-slit experiment with monochromatic light, fringes are obtained on a screen placed at some distance from the plane of slits. If the screen is moved by 5 × 10-2 m towards the slits, the change in fringe width is 3 × 10-3 cm. If the distance between the slits is 1 mm, then the wavelength of the light will be ______ nm.
In a Young's double slit experiment, the width of the one of the slit is three times the other slit. The amplitude of the light coming from a slit is proportional to the slit- width. Find the ratio of the maximum to the minimum intensity in the interference pattern.
The central fringe of the interference pattern produced by the light of wavelength 6000 Å is found to shift to the position of the fourth bright fringe after a glass plate of refractive index 1.5 is introduced in the path of one of the beams. The thickness of the glass plate would be ______.
In Young's double slit experiment the two slits are 0.6 mm distance apart. Interference pattern is observed on a screen at a distance 80 cm from the slits. The first dark fringe is observed on the screen directly opposite to one of the slits. The wavelength of light will be ______ nm.
The maximum number of possible interference maxima for slit-separation equal to twice the wavelength in Young's double-slit experiment is ______.
