Advertisements
Advertisements
Question
In a Young’s double slit experiment, the source is white light. One of the holes is covered by a red filter and another by a blue filter. In this case ______.
Options
there shall be alternate interference patterns of red and blue.
there shall be an interference pattern for red distinct from that for blue.
there shall be no interference fringes.
there shall be an interference pattern for red mixing with one for blue.
Solution
In a Young’s double slit experiment, the source is white light. One of the holes is covered by a red filter and another by a blue filter. In this case there shall be no interference fringes.
Explanation:
Condition for Observing Interference
The initial phase difference between the interfering waves must remain constant. Otherwise, the interference will not be sustained.
The frequency and wavelengths of two waves should be equal. If not the phase difference will not remain constant and so the interference will not be sustained.
The light must be monochromatic. This eliminates overlapping of patterns as each wavelength corresponds to one interference pattern.
Here in this problem of Young’s double-slit experiment, when one of the holes is covered by a red filter and another by a blue filter. In this case, due to filtration only red and blue lights are present. In YDSE monochromatic light is used for the formation of fringes on the screen. Hence, in this case there shall be no interference fringes.
The wavefront emitted by a narrow source is divided in two parts reflection, refraction or diffraction. The coherent sources so obtained are imaginary.
APPEARS IN
RELATED QUESTIONS
In Young' s experiment the ratio of intensity at the maxima and minima . in the interference pattern is 36 : 16. What is the ratio of the widths of the two slits?
What is the effect on the fringe width if the distance between the slits is reduced keeping other parameters same?
In Young's double slit experiment, describe briefly how bright and dark fringes are obtained on the screen kept in front of a double slit. Hence obtain the expression for the fringe width.
In a double-slit experiment the angular width of a fringe is found to be 0.2° on a screen placed 1 m away. The wavelength of light used is 600 nm. What will be the angular width of the fringe if the entire experimental apparatus is immersed in water? Take refractive index of water to be 4/3.
The slits in a Young's double slit experiment have equal width and the source is placed symmetrically with respect to the slits. The intensity at the central fringe is I0. If one of the slits is closed, the intensity at this point will be ____________ .
In a Young's double slit experiment, using monochromatic light, the fringe pattern shifts by a certain distance on the screen when a mica sheet of refractive index 1.6 and thickness 1.964 micron (1 micron = 10−6 m) is introduced in the path of one of the interfering waves. The mica sheet is then removed and the distance between the screen and the slits is doubled. It is found that the distance between the successive maxima now is the same as the observed fringe-shift upon the introduction of the mica sheet. Calculate the wavelength of the monochromatic light used in the experiment.
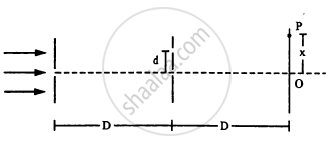
Consider the arrangement shown in the figure. The distance D is large compared to the separation d between the slits.
- Find the minimum value of d so that there is a dark fringe at O.
- Suppose d has this value. Find the distance x at which the next bright fringe is formed.
- Find the fringe-width.
In a Young's double slit interference experiment, the fringe pattern is observed on a screen placed at a distance D from the slits. The slits are separated by a distance d and are illuminated by monochromatic light of wavelength \[\lambda.\] Find the distance from the central point where the intensity falls to (a) half the maximum, (b) one-fourth the maximum.
In Young’s double-slit experiment, using monochromatic light, fringes are obtained on a screen placed at some distance from the slits. If the screen is moved by 5 x 10-2 m towards the slits, the change in the fringe width is 3 x 10-5 m. If the distance between the two slits is 10-3 m, calculate the wavelength of the light used.
In Young's double slit experiment, show that:
`β = (λ"D")/"d"`
Where the terms have their usual meaning.
