Advertisements
Advertisements
Question
Consider a ray of light incident from air onto a slab of glass (refractive index n) of width d, at an angle θ. The phase difference between the ray reflected by the top surface of the glass and the bottom surface is ______.
Options
`(4πd)/λ (1 - 1/n^2 sin^2 θ)^(1/2) + π`
`(4πd)/λ (1 - 1/n^2 sin^2 θ)^(1/2)`
`(4πd)/λ (1 - 1/n^2 sin^2 θ)^(1/2) + π/2`
`(4πd)/λ (1 - 1/n^2 sin^2 θ)^(1/2) + 2π`
Advertisements
Solution
Consider a ray of light incident from air onto a slab of glass (refractive index n) of width d, at an angle θ. The phase difference between the ray reflected by the top surface of the glass and the bottom surface is `underline((4πd)/λ (1 - 1/n^2 sin^2 θ)^(1/2) + π)`.
Explanation:
If slab of a glass is placed in air, the wave reflected from the upper surface (from a denser medium) sutlers a sudden phase change of π, while the wave reflected from the lower surface (from a rarer medium) suffers no such phase change.
It is useful to draw an analogy between reflected light waves and the reflections of a transverse wave on a stretched string when the wave meets a boundary:
Figure (a) shows that ray reflecting from a medium of higher refractive index undergoes a 180° phase change.
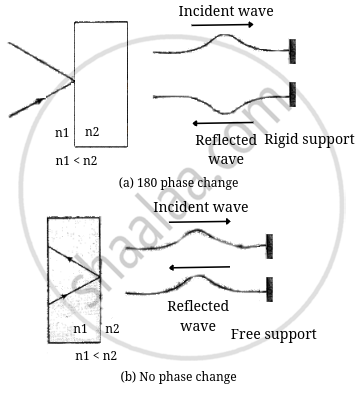
Now consider the diagram, the ray (P) is incident at an angle θ and gets reflected in the direction P' and refracted in the direction P". Due to reflection from the glass medium, there is a phase change of π.
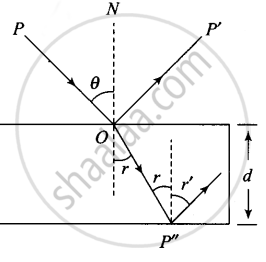
Time taken to travel along OP"
Δt = `(OP^")/v = (d/(cos r))/(c/n) = (nd)/(c cos r)`
From Snell's law, n = `sin θ/sin r`
⇒ `sin r = sin θ/n`
`cos r = sqrt(1 - sin^2r) = sqrt(1 - (sin^2θ)/v^2)`
Phase difference, `Δphi = (2pi)/T xx Δt` ⇒ `Δphi = (2pind)/λ (1 - (sin^2θ)/n^2)^(-1/2)`
So, net phase difference = `Δphi + pi`
⇒ `Δphi_("net") = (4pid)/λ (1 - 1/n^2 sin^2θ) + pi`
APPEARS IN
RELATED QUESTIONS
As you have learnt in the text, the principle of linear superposition of wave displacement is basic to understanding intensity distributions in diffraction and interference patterns. What is the justification of this principle?
A tuning fork of frequency 480 Hz is used to vibrate a sonometer wire having natural frequency 240 Hz. The wire will vibrate with a frequency of
A tuning fork of frequency 480 Hz is used to vibrate a sonometer wire having natural frequency 410 Hz. The wire will vibrate with a frequency
A heavy ball is suspended from the ceiling of a motor car through a light string. A transverse pulse travels at a speed of 60 cm s −1 on the string when the car is at rest and 62 cm s−1 when the car accelerates on a horizontal road. Find the acceleration of the car. Take g = 10 m s−2
Two waves, each having a frequency of 100 Hz and a wavelength of 2⋅0 cm, are travelling in the same direction on a string. What is the phase difference between the waves (a) if the second wave was produced 0⋅015 s later than the first one at the same place, (b) if the two waves were produced at the same instant but first one was produced a distance 4⋅0 cm behind the second one? (c) If each of the waves has an amplitude of 2⋅0 mm, what would be the amplitudes of the resultant waves in part (a) and (b) ?
Answer briefly.
State and explain the principle of superposition of waves.
The energy in the superposition of waves ____________.
Three identical charges are placed on three vertices of a square. If the force acting between q1 and q2 is F12 and between q1 and q3 is f13 then `"F"_13/"F"_12` = ____________.
Two particles P and Q describe simple harmonic motions of same amplitude a, frequency v along the same straight line. The maximum distance between the two particles is a`sqrt(2)`. The initial phase difference between the particles is
The wavelength of light used in young.'s double slit experiment is λ. The intensity at a point on the screen is I where the path difference is λ/6. If I0 denotes the maximum intensity, then the ratio of I and I0 is ______.
The displacement of an elastic wave is given by the function y = 3 sin ωt + 4 cos ωt. where y is in cm and t is in second. Calculate the resultant amplitude.
For the harmonic travelling wave y = 2 cos 2π (10t – 0.0080x + 3.5) where x and y are in cm and t is second. What is the phase difference between the oscillatory motion at two points separated by a distance of 4 m.
For the harmonic travelling wave y = 2 cos 2π (10t – 0.0080x + 3.5) where x and y are in cm and t is second. What is the phase difference between the oscillatory motion at two points separated by a distance of 0.5 m
For the harmonic travelling wave y = 2 cos 2π (10t – 0.0080x + 3.5) where x and y are in cm and t is second. What is the phase difference between the oscillatory motion at two points separated by a distance of `λ/2`
For the harmonic travelling wave y = 2 cos 2π (10t – 0.0080x + 3.5) where x and y are in cm and t is second. What is the phase difference between the oscillatory motion at two points separated by a distance of What is the phase difference between the oscillation of a particle located at x = 100 cm, at t = T s and t = 5 s?
In the interference of two sources of intensities I0 and 9I0 the intensity at a point where the phase difference is `pi/2` is ______.
In Young's double-slit experiment, the intensity at a point where the path difference is `lambda/4` is l. If the maximum intensity is l0, and then the ratio of `l_0/l` is ______.
`(cos45^circ = 1/sqrt2 = sin45^circ)`
When two coherent monochromatic light beams of intensities I and 4I are superimposed, then what are the maximum and minimum possible intensities in the resulting beams?
