Advertisements
Advertisements
Question
In Young’s double-slit experiment, using monochromatic light, fringes are obtained on a screen placed at some distance from the slits. If the screen is moved by 5 x 10-2 m towards the slits, the change in the fringe width is 3 x 10-5 m. If the distance between the two slits is 10-3 m, calculate the wavelength of the light used.
Solution
Here, ΔD = 5 x 10-2 m, Δβ = 3 ×10-5 m, d = 10-3 m, λ = ?
We know that fringe width in Young’s double-slit experiment is given by
`"β" = λ "D"/"d"`
Here, since λ and d are constant, we can write
`"Δβ" = λ/"d" "ΔD"`
∴ λ = `"Δβ"/"ΔD" d`
λ = `( 3 xx 10^-5 xx 10^-3)/(5 xx 10^-2)`
λ = `0.6 xx 10^-6 m xx 10^-7 m = 6000Å `
APPEARS IN
RELATED QUESTIONS
Derive an expression for path difference in Young’s double slit experiment and obtain the conditions for constructive and destructive interference at a point on the screen.
Find the intensity at a point on a screen in Young's double slit experiment where the interfering waves have a path difference of (i) λ/6, and (ii) λ/2.
Write three characteristic features to distinguish between the interference fringes in Young's double slit experiment and the diffraction pattern obtained due to a narrow single slit.
A parallel beam of light of wavelength 500 nm falls on a narrow slit and the resulting diffraction pattern is observed on a screen 1 m away. It is observed that the first minimum is a distance of 2.5 mm away from the centre. Find the width of the slit.
Draw the intensity distribution as function of phase angle when diffraction of light takes place through coherently illuminated single slit.
The force required to double the length of a steel wire of area 1 cm2, if its Young's modulus Y= 2 × 1011/m2 is:
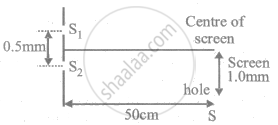
In Young's double slit experiment shown in figure S1 and S2 are coherent sources and S is the screen having a hole at a point 1.0 mm away from the central line. White light (400 to 700 nm) is sent through the slits. Which wavelength passing through the hole has strong intensity?
In a double-slit experiment with monochromatic light, fringes are obtained on a screen placed at some distance from the plane of slits. If the screen is moved by 5 × 10-2 m towards the slits, the change in fringe width is 3 × 10-3 cm. If the distance between the slits is 1 mm, then the wavelength of the light will be ______ nm.
A fringe width of 6 mm was produced for two slits separated by 1 mm apart. The screen is placed 10 m away. The wavelength of light used is 'x' nm. The value of 'x' to the nearest integer is ______.
The central fringe of the interference pattern produced by the light of wavelength 6000 Å is found to shift to the position of the fourth bright fringe after a glass plate of refractive index 1.5 is introduced in the path of one of the beams. The thickness of the glass plate would be ______.
