Advertisements
Advertisements
Question
Derive an expression for path difference in Young’s double slit experiment and obtain the conditions for constructive and destructive interference at a point on the screen.
Solution
Diagrammatical arrangement for Young’s double slit experiment:
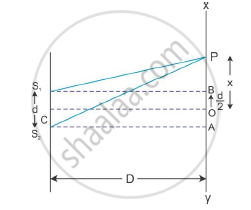
In the above figure, S1 and S2 are two narrow closely spaced slits illuminated by monochromatic light of wavelength λ. The screen on which the interference pattern is observed is represented as XY.
If S1 and S2 emit light in the same phase, then for point O, the path difference receives light in the same phase. The superposition at O is constructive producing a bright point called the central maxima. The intensity at any point P at a distance x from O depends on the path difference between light reaching P from S1 and S2. The path difference is S2P − S1P.
From the geometry of the figure, we have
`(S_2P)^2=D^2+(x+d/2)^2`
Similarly, we have
`(S_1P)^2=D^2+(x+d/2)^2`
`:.(S_2P)^2-(S_1P)^2=D^2+(x+d/2)^2-D^2-(x-d/2)^2`
`:.(S_2P)^2-(S_1P)^2=(x+d/2)^2-(x-d/2)^2`
`:.(S_2P)^2-(S_1P)^2=x^2+xd+d^2/4-x^2+xd-d^2/4`
∴ (S2P)2-(S1P)2=2xd
∴(S2P-S1P)(S2P+S1P)=2xd
`:.S_2P-S_1P=(2xd)/(S_2P+S_1P)`
Now, from the figure we can see that
S2P≈S1P = D
`:.S_2P-S_1P=(2xd)/(2D)=(xd)/D`
This is the expression for path difference.
Condition for constructive interference: Constructive interference will occur when the phase difference between the two superposing waves is an even multiple of π or the path difference is an integral multiple of wavelength λ.
Condition for destructive interference: Destructive interference will occur when the phase difference between the two superposing waves is an odd multiple of π or the path difference is an odd multiple of wavelength λ/2.
RELATED QUESTIONS
The intensity at the central maxima in Young’s double slit experiment is I0. Find out the intensity at a point where the path difference is` lambda/6,lambda/4 and lambda/3.`
Show that the fringe pattern on the screen is actually a superposition of slit diffraction from each slit.
What is the effect on the fringe width if the distance between the slits is reduced keeping other parameters same?
In a double-slit experiment using the light of wavelength 600 nm, the angular width of the fringe formed on a distant screen is 0.1°. Find the spacing between the two slits.
A beam of light consisting of two wavelengths, 650 nm and 520 nm, is used to obtain interference fringes in a Young’s double-slit experiment.
Find the distance of the third bright fringe on the screen from the central maximum for wavelength 650 nm.
A beam of light consisting of two wavelengths, 650 nm and 520 nm, is used to obtain interference fringes in a Young’s double-slit experiment.
What is the least distance from the central maximum where the bright fringes due to both the wavelengths coincide?
In Young’s experiment, the ratio of intensity at the maxima and minima in an interference
pattern is 36 : 9. What will be the ratio of the intensities of two interfering waves?
Write three characteristic features to distinguish between the interference fringes in Young's double slit experiment and the diffraction pattern obtained due to a narrow single slit.
In Young’s double slit experiment using monochromatic light of wavelength λ, the intensity of light at a point on the screen where path difference is λ, is K units. Find out the intensity of light at a point where path difference is λ/3.
A beam of light consisting of two wavelengths, 800 nm and 600 nm is used to obtain the interference fringes in a Young's double slit experiment on a screen placed 1 · 4 m away. If the two slits are separated by 0·28 mm, calculate the least distance from the central bright maximum where the bright fringes of the two wavelengths coincide.
What is the effect on the interference fringes to a Young’s double slit experiment when
(i) the separation between the two slits is decreased?
(ii) the width of a source slit is increased?
(iii) the monochromatic source is replaced by a source of white light?
Justify your answer in each case.
How does the fringe width get affected, if the entire experimental apparatus of Young is immersed in water?
The slits in a Young's double slit experiment have equal width and the source is placed symmetrically with respect to the slits. The intensity at the central fringe is I0. If one of the slits is closed, the intensity at this point will be ____________ .
White light is used in a Young's double slit experiment. Find the minimum order of the violet fringe \[\left( \lambda = 400\text{ nm} \right)\] which overlaps with a red fringe \[\left( \lambda = 700\text{ nm} \right).\]
A transparent paper (refractive index = 1.45) of thickness 0.02 mm is pasted on one of the slits of a Young's double slit experiment which uses monochromatic light of wavelength 620 nm. How many fringes will cross through the centre if the paper is removed?
Two transparent slabs having equal thickness but different refractive indices µ1 and µ2are pasted side by side to form a composite slab. This slab is placed just after the double slit in a Young's experiment so that the light from one slit goes through one material and the light from the other slit goes through the other material. What should be the minimum thickness of the slab so that there is a minimum at the point P0 which is equidistant from the slits?
A thin paper of thickness 0.02 mm having a refractive index 1.45 is pasted across one of the slits in a Young's double slit experiment. The paper transmits 4/9 of the light energy falling on it. (a) Find the ratio of the maximum intensity to the minimum intensity in the fringe pattern. (b) How many fringes will cross through the centre if an identical paper piece is pasted on the other slit also? The wavelength of the light used is 600 nm.
In a Young's double slit experiment, \[\lambda = 500\text{ nm, d = 1.0 mm and D = 1.0 m.}\] Find the minimum distance from the central maximum for which the intensity is half of the maximum intensity.
What should be the path difference between two waves reaching a point for obtaining constructive interference in Young’s Double Slit experiment ?
How is the fringe width of an interference pattern in Young's double-slit experiment affected if the two slits are brought closer to each other?
In Young’s double-slit experiment, show that:
`beta = (lambda "D")/"d"` where the terms have their usual meaning.
Draw the intensity distribution as function of phase angle when diffraction of light takes place through coherently illuminated single slit.
An unpolarised beam of intensity 2a2 passes through a thin polaroid. Assuming zero absorption in the polaroid, the intensity of emergent plane polarised light will be
A projectile can have the same range R for two angles of projection. If t1 and t2 be the times of flight in two cases, then what is the product of two times of flight?
Young's double slit experiment is made in a liquid. The 10th bright fringe lies in liquid where 6th dark fringe lies in vacuum. The refractive index of the liquid is approximately
In Young's double slit experiment, the minimum amplitude is obtained when the phase difference of super-imposing waves is: (where n = 1, 2, 3, ...)
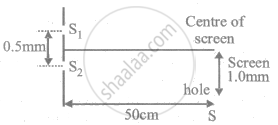
In Young's double slit experiment shown in figure S1 and S2 are coherent sources and S is the screen having a hole at a point 1.0 mm away from the central line. White light (400 to 700 nm) is sent through the slits. Which wavelength passing through the hole has strong intensity?
In a Young’s double slit experiment, the source is white light. One of the holes is covered by a red filter and another by a blue filter. In this case ______.
Consider a two-slit interference arrangement (Figure) such that the distance of the screen from the slits is half the distance between the slits. Obtain the value of D in terms of λ such that the first minima on the screen falls at a distance D from the centre O.
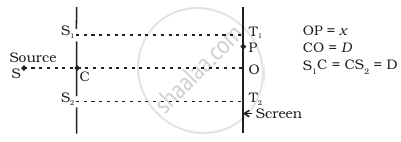
ASSERTION (A): In an interference pattern observed in Young's double slit experiment, if the separation (d) between coherent sources as well as the distance (D) of the screen from the coherent sources both are reduced to 1/3rd, then new fringe width remains the same.
REASON (R): Fringe width is proportional to (d/D).
How will the interference pattern in Young's double-slit experiment be affected if the phase difference between the light waves emanating from the two slits S1 and S2 changes from 0 to π and remains constant?
In Young's double slit experiment using light of wavelength 600 nm, the slit separation is 0.8 mm and the screen is kept 1.6 m from the plane of the slits. Calculate
- the fringe width
- the distance of (a) third minimum and (b) fifth maximum, from the central maximum.
A beam of light consisting of two wavelengths 600 nm and 500 nm is used in Young's double slit experiment. The silt separation is 1.0 mm and the screen is kept 0.60 m away from the plane of the slits. Calculate:
- the distance of the second bright fringe from the central maximum for wavelength 500 nm, and
- the least distance from the central maximum where the bright fringes due to both wavelengths coincide.
In Young's double slit experiment the two slits are 0.6 mm distance apart. Interference pattern is observed on a screen at a distance 80 cm from the slits. The first dark fringe is observed on the screen directly opposite to one of the slits. The wavelength of light will be ______ nm.
In Young's double slit experiment, the distance of the 4th bright fringe from the centre of the interference pattern is 1.5 mm. The distance between the slits and the screen is 1.5 m, and the wavelength of light used is 500 nm. Calculate the distance between the two slits.
In Young’s double slit experiment, how is interference pattern affected when the following changes are made:
- Slits are brought closer to each other.
- Screen is moved away from the slits.
- Red coloured light is replaced with blue coloured light.
