Advertisements
Advertisements
Question
Show that the fringe pattern on the screen is actually a superposition of slit diffraction from each slit.
Solution
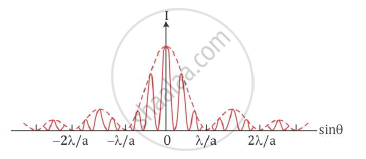
The intensity variation in the fringe pattern obtained on a screen in a Young’s double slit experiment corresponds to both single slit diffraction and double slit interference because the two sources are slits of finite width in the double slit experiment.
If a lens is placed in front of the double slits and when one of the slit S1 is closed and the other kept open, a single slit diffraction is formed on the screen. A similar diffraction pattern is obtained on the screen if the slit S1 is kept open and S2 is closed. Both diffraction patterns form on the same position on the screen in the focal plane of the lens. When both slits open simultaneously, the resulting total intensity pattern on the screen is actually the superposition of the single slit diffraction pattern formed by waves from various point sources of each slit and a double slit interference pattern as shown. The actual double slit intensity pattern consists of the interference pattern (solid lines) formed within the diffraction pattern (dotted lines).
APPEARS IN
RELATED QUESTIONS
Can we perform Young's double slit experiment with sound waves? To get a reasonable "fringe pattern", what should be the order of separation between the slits? How can the bright fringes and the dark fringes be detected in this case?
A double slit S1 − S2 is illuminated by a coherent light of wavelength \[\lambda.\] The slits are separated by a distance d. A plane mirror is placed in front of the double slit at a distance D1 from it and a screen ∑ is placed behind the double slit at a distance D2 from it (see the following figure). The screen ∑ receives only the light reflected by the mirror. Find the fringe-width of the interference pattern on the screen.
How is the fringe width of an interference pattern in Young's double-slit experiment affected if the two slits are brought closer to each other?
In Young's double slit experiment using monochromatic light of wavelength 600 nm, 5th bright fringe is at a distance of 0·48 mm from the centre of the pattern. If the screen is at a distance of 80 cm from the plane of the two slits, calculate:
(i) Distance between the two slits.
(ii) Fringe width, i.e. fringe separation.
In Young's double slit experiment the slits are 0.589 mm apart and the interference is observed on a screen placed at a distance of 100 cm from the slits. It is found that the 9th bright fringe is at a distance of 7.5 mm from the dark fringe which is second from the center of the fringe pattern. Find the wavelength of the light used.
A projectile can have the same range R for two angles of projection. If t1 and t2 be the times of flight in two cases, then what is the product of two times of flight?
The Young's double slit experiment is performed with blue and with green light of wavelengths 4360Å and 5460Å respectively. If x is the distance of 4th maxima from the central one, then:
A slit of width 0.6 mm is illuminated by a beam of light consisting of two wavelengths 600 nm and 480 nm. The diffraction pattern is observed on a screen 1.0 m from the slit. Find:
- The distance of the second bright fringe from the central maximum pertaining to the light of 600 nm.
- The least distance from the central maximum at which bright fringes due to both wavelengths coincide.
In a double-slit experiment with monochromatic light, fringes are obtained on a screen placed at some distance from the plane of slits. If the screen is moved by 5 × 10-2 m towards the slits, the change in fringe width is 3 × 10-3 cm. If the distance between the slits is 1 mm, then the wavelength of the light will be ______ nm.
Two beams of light having intensities I and 41 interfere to produce a fringe pattern on a screen. The phase difference between the two beams are π/2 and π/3 at points A and B respectively. The difference between the resultant intensities at the two points is xl. The value of x will be ______.
