Advertisements
Advertisements
Question
In Young's double slit experiment using monochromatic light of wavelength 600 nm, 5th bright fringe is at a distance of 0·48 mm from the centre of the pattern. If the screen is at a distance of 80 cm from the plane of the two slits, calculate:
(i) Distance between the two slits.
(ii) Fringe width, i.e. fringe separation.
Solution
(i) `lambda = 600nm = 600/1000000 mm`
`lambda =6 xx 10^-4 `mm
D = Distance of slits from the screen = 80cm
⇒ D = 800 mm
`beta` = Fringe - width
`5beta = 0.48` mm
∴ `beta = 0.48/5`
(ii) `beta = 0.096` mm
d = distance between 2 slits
` beta = (lambdaD)/d`
`0.48/5 = (6xx10^-4 xx 8xx10^2)/d`
⇒ `d = (6 xx8xx10^-2 xx5xx10^2)/48 = 5` mm
APPEARS IN
RELATED QUESTIONS
The fringes produced in diffraction pattern are of _______.
(A) equal width with same intensity
(B) unequal width with varying intensity
(C) equal intensity\
(D) equal width with varying intensity
Write three characteristic features to distinguish between the interference fringes in Young's double slit experiment and the diffraction pattern obtained due to a narrow single slit.
In Young’s double slit experiment to produce interference pattern, obtain the conditions for constructive and destructive interference. Hence deduce the expression for the fringe width.
If the separation between the slits in a Young's double slit experiment is increased, what happens to the fringe-width? If the separation is increased too much, will the fringe pattern remain detectable?
In a Young's double slit experiment, using monochromatic light, the fringe pattern shifts by a certain distance on the screen when a mica sheet of refractive index 1.6 and thickness 1.964 micron (1 micron = 10−6 m) is introduced in the path of one of the interfering waves. The mica sheet is then removed and the distance between the screen and the slits is doubled. It is found that the distance between the successive maxima now is the same as the observed fringe-shift upon the introduction of the mica sheet. Calculate the wavelength of the monochromatic light used in the experiment.
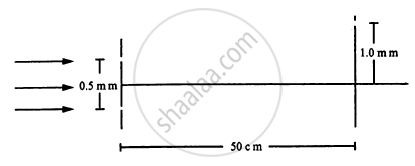
White coherent light (400 nm-700 nm) is sent through the slits of a Young's double slit experiment (see the following figure). The separation between the slits is 0⋅5 mm and the screen is 50 cm away from the slits. There is a hole in the screen at a point 1⋅0 mm away (along the width of the fringes) from the central line. (a) Which wavelength(s) will be absent in the light coming from the hole? (b) Which wavelength(s) will have a strong intensity?
In a Young’s double slit experiment, the source is white light. One of the holes is covered by a red filter and another by a blue filter. In this case ______.
In Young's double slit experiment using light of wavelength 600 nm, the slit separation is 0.8 mm and the screen is kept 1.6 m from the plane of the slits. Calculate
- the fringe width
- the distance of (a) third minimum and (b) fifth maximum, from the central maximum.
Using Young’s double slit experiment, a monochromatic light of wavelength 5000Å produces fringes of fringe width 0.5 mm. If another monochromatic light of wavelength 6000Å is used and the separation between the slits is doubled, then the new fringe width will be ______.
The central fringe of the interference pattern produced by the light of wavelength 6000 Å is found to shift to the position of the fourth bright fringe after a glass plate of refractive index 1.5 is introduced in the path of one of the beams. The thickness of the glass plate would be ______.
