Advertisements
Advertisements
Question
The fringes produced in diffraction pattern are of _______.
(A) equal width with same intensity
(B) unequal width with varying intensity
(C) equal intensity\
(D) equal width with varying intensity
Solution
unequal width with varying intensity
APPEARS IN
RELATED QUESTIONS
The intensity at the central maxima in Young’s double slit experiment is I0. Find out the intensity at a point where the path difference is` lambda/6,lambda/4 and lambda/3.`
In young’s double slit experiment, deduce the conditions for obtaining constructive and destructive interference fringes. Hence, deduce the expression for the fringe width.
Show that the fringe pattern on the screen is actually a superposition of slit diffraction from each slit.
In a double-slit experiment using the light of wavelength 600 nm, the angular width of the fringe formed on a distant screen is 0.1°. Find the spacing between the two slits.
Using analytical method for interference bands, obtain an expression for path difference between two light waves.
In Young’s experiment, the ratio of intensity at the maxima and minima in an interference
pattern is 36 : 9. What will be the ratio of the intensities of two interfering waves?
Explain two features to distinguish between the interference pattern in Young's double slit experiment with the diffraction pattern obtained due to a single slit.
In Young’s double slit experiment, show graphically how the intensity of light varies with distance
Write three characteristic features to distinguish between the interference fringes in Young's double slit experiment and the diffraction pattern obtained due to a narrow single slit.
How does the fringe width get affected, if the entire experimental apparatus of Young is immersed in water?
In Young’s experiment interference bands were produced on a screen placed at 150 cm from two slits, 0.15 mm apart and illuminated by the light of wavelength 6500 Å. Calculate the fringe width.
Two coherent sources of light having intensity ratio 81 : 1 produce interference fringes. Calculate the ratio of intensities at the maxima and minima in the interference pattern.
Suppose white light falls on a double slit but one slit is covered by a violet filter (allowing λ = 400 nm). Describe the nature of the fringe pattern observed.
A transparent paper (refractive index = 1.45) of thickness 0.02 mm is pasted on one of the slits of a Young's double slit experiment which uses monochromatic light of wavelength 620 nm. How many fringes will cross through the centre if the paper is removed?
In a Young's double slit experiment, using monochromatic light, the fringe pattern shifts by a certain distance on the screen when a mica sheet of refractive index 1.6 and thickness 1.964 micron (1 micron = 10−6 m) is introduced in the path of one of the interfering waves. The mica sheet is then removed and the distance between the screen and the slits is doubled. It is found that the distance between the successive maxima now is the same as the observed fringe-shift upon the introduction of the mica sheet. Calculate the wavelength of the monochromatic light used in the experiment.
A parallel beam of monochromatic light is used in a Young's double slit experiment. The slits are separated by a distance d and the screen is placed parallel to the plane of the slits. Slow that if the incident beam makes an angle \[\theta = \sin^{- 1} \left( \frac{\lambda}{2d} \right)\] with the normal to the plane of the slits, there will be a dark fringe at the centre P0 of the pattern.
A double slit S1 − S2 is illuminated by a coherent light of wavelength \[\lambda.\] The slits are separated by a distance d. A plane mirror is placed in front of the double slit at a distance D1 from it and a screen ∑ is placed behind the double slit at a distance D2 from it (see the following figure). The screen ∑ receives only the light reflected by the mirror. Find the fringe-width of the interference pattern on the screen.
Consider the arrangement shown in the figure. By some mechanism, the separation between the slits S3 and S4 can be changed. The intensity is measured at the point P, which is at the common perpendicular bisector of S1S2 and S2S4. When \[z = \frac{D\lambda}{2d},\] the intensity measured at P is I. Find the intensity when z is equal to

(a) \[\frac{D\lambda}{d}\]
(b) \[\frac{3D\lambda}{2d}\] and
(c) \[\frac{2D\lambda}{d}\]
In Young’s double-slit experiment, show that:
`beta = (lambda "D")/"d"` where the terms have their usual meaning.
Wavefront is ______.
In Young’s double slit experiment, what should be the phase difference between the two overlapping waves to obtain 5th dark band/fringe on the screen?
"If the slits in Young's double slit experiment are identical, then intensity at any point on the screen may vary between zero and four times to the intensity due to single slit".
Justify the above statement through a relevant mathematical expression.
An unpolarised beam of intensity 2a2 passes through a thin polaroid. Assuming zero absorption in the polaroid, the intensity of emergent plane polarised light will be
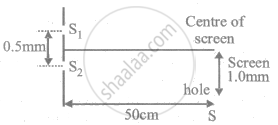
In Young's double slit experiment shown in figure S1 and S2 are coherent sources and S is the screen having a hole at a point 1.0 mm away from the central line. White light (400 to 700 nm) is sent through the slits. Which wavelength passing through the hole has strong intensity?
In a Young’s double slit experiment, the source is white light. One of the holes is covered by a red filter and another by a blue filter. In this case ______.
How will the interference pattern in Young's double-slit experiment be affected if the source slit is moved away from the plane of the slits?
In a double-slit experiment with monochromatic light, fringes are obtained on a screen placed at some distance from the plane of slits. If the screen is moved by 5 × 10-2 m towards the slits, the change in fringe width is 3 × 10-3 cm. If the distance between the slits is 1 mm, then the wavelength of the light will be ______ nm.
A fringe width of 6 mm was produced for two slits separated by 1 mm apart. The screen is placed 10 m away. The wavelength of light used is 'x' nm. The value of 'x' to the nearest integer is ______.
The maximum number of possible interference maxima for slit-separation equal to twice the wavelength in Young's double-slit experiment is ______.
In Young's double slit experiment, the distance of the 4th bright fringe from the centre of the interference pattern is 1.5 mm. The distance between the slits and the screen is 1.5 m, and the wavelength of light used is 500 nm. Calculate the distance between the two slits.
