Question

Consider the arrangement shown in the figure. By some mechanism, the separation between the slits S₃ and S₄ can be changed. The intensity is measured at the point P, which is at the common perpendicular bisector of S₁S₂ and S₂S₄. When \[z = \frac{D\lambda}{2d},\] the intensity measured at P is I. Find the intensity when z is equal to

(a) \[\frac{D\lambda}{d}\]

(b) \[\frac{3D\lambda}{2d}\]  and

(c) \[\frac{2D\lambda}{d}\]

Answer 1

Given:-

Fours slits S₁, S₂, S₃ and S₄.

The separation between slits S₃ and S₄ can be changed.

Point P is the common perpendicular bisector of S₁S₂ and S₃S₄.

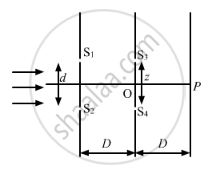
(a) For \[z = \frac{\lambda D}{d}\]

The position of the slits from the central point of the first screen is given by \[y =  {OS}_3  =  {OS}_4  = \frac{z}{2} = \frac{\lambda D}{2d}\]

The corresponding path difference in wave fronts reaching S₃ is given by \[∆ x = \frac{yd}{D} = \frac{\lambda D}{2d} \times \frac{d}{D} = \frac{\lambda}{2}\]

Similarly at S₄, path difference, \[∆ x = \frac{yd}{D} = \frac{\lambda D}{2d} \times \frac{d}{D} = \frac{\lambda}{2}\]

i.e. dark fringes are formed at S₃ and S₄.

So, the intensity of light at S₃ and S₄ is zero. Hence, the intensity at P is also zero.

(b) For \[z = \frac{3\lambda D}{2d}\]

The position of the slits from the central point of the first screen is given by \[y =  {OS}_3  =  {OS}_4  = \frac{z}{2} = \frac{3\lambda D}{4d}\]

The corresponding path difference in wave fronts reaching S₃ is given by \[∆ x = \frac{yd}{D} = \frac{3\lambda D}{4d} \times \frac{d}{D} = \frac{3\lambda}{4}\]

Similarly at S₄, path difference,

\[∆ x = \frac{yd}{D} = \frac{3\lambda D}{4d} \times \frac{d}{D} = \frac{3\lambda}{4}\]

Hence, the intensity at P is I.

(c) For \[z = \frac{2\lambda D}{d}\]

The position of the slits from the central point of the first screen is given by \[y =  {OS}_3  =  {OS}_4  = \frac{z}{2} = \frac{2\lambda D}{2d}\]

The corresponding path difference in wave fronts reaching S₃ is given by \[∆ x = \frac{yd}{D} = \frac{2\lambda D}{2d} \times \frac{d}{D} = \lambda\]

Similarly at S₄, path difference, \[∆ x = \frac{yd}{D} = \frac{2\lambda D}{2d} \times \frac{d}{D} = \lambda\]

Hence, the intensity at P is 2I.