Advertisements
Advertisements
Question
Show that the angular width of the first diffraction fringe is half that of the central fringe.
Solution
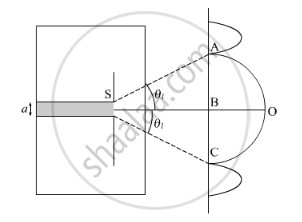
Let λ and a be the wavelength and slit width of diffracting system, respectively. Let O be the position of central maximum. Condition for the first minimum is given by
asinθ=mλ .....(1)
Let θ be the angle of diffraction.
As diffraction angle is small
∴ sinθ ≈ θ
For the first diffraction minimum, let θ = θ1
For the first minimum, take m =1
aθ1=λ
`=>theta_1=lambda/a`
Now, angular width AB = θ1
Angular width BC = θ1
Angular width AC = 2θ1
Width of central maximum = 2θ1
APPEARS IN
RELATED QUESTIONS
The intensity at the central maxima in Young’s double slit experiment is I0. Find out the intensity at a point where the path difference is` lambda/6,lambda/4 and lambda/3.`
Write two characteristics features distinguish the diffractions pattern from the interference fringes obtained in Young’s double slit experiment.
How does the fringe width get affected, if the entire experimental apparatus of Young is immersed in water?
In Young’s experiment interference bands were produced on a screen placed at 150 cm from two slits, 0.15 mm apart and illuminated by the light of wavelength 6500 Å. Calculate the fringe width.
In a Young's double slit interference experiment, the fringe pattern is observed on a screen placed at a distance D from the slits. The slits are separated by a distance d and are illuminated by monochromatic light of wavelength \[\lambda.\] Find the distance from the central point where the intensity falls to (a) half the maximum, (b) one-fourth the maximum.
"If the slits in Young's double slit experiment are identical, then intensity at any point on the screen may vary between zero and four times to the intensity due to single slit".
Justify the above statement through a relevant mathematical expression.
The Young's double slit experiment is performed with blue and with green light of wavelengths 4360Å and 5460Å respectively. If x is the distance of 4th maxima from the central one, then:
A slit of width 0.6 mm is illuminated by a beam of light consisting of two wavelengths 600 nm and 480 nm. The diffraction pattern is observed on a screen 1.0 m from the slit. Find:
- The distance of the second bright fringe from the central maximum pertaining to the light of 600 nm.
- The least distance from the central maximum at which bright fringes due to both wavelengths coincide.
Interference fringes are observed on a screen by illuminating two thin slits 1 mm apart with a light source (λ = 632.8 nm). The distance between the screen and the slits is 100 cm. If a bright fringe is observed on a screen at distance of 1.27 mm from the central bright fringe, then the path difference between the waves, which are reaching this point from the slits is close to :
In Young's double-slit experiment, the separation between the two slits is d and the distance of the screen from the slits is 1000 d. If the first minima fall at a distance d from the central maximum, obtain the relation between d and λ.
