Advertisements
Advertisements
Question
In Young’s double-slit experiment, show that:
`beta = (lambda "D")/"d"` where the terms have their usual meaning.
Solution
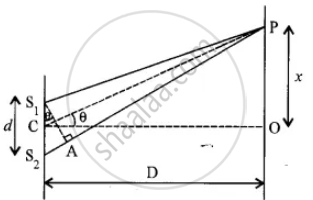
d = Distance between the slits
D = Distance between slit and screen
'P' is the position of mth order bright fringe.
From diagram, the path difference p is
S2P - S1P = S2P - AP
= S2A
`"sin"theta = ("S"_2"A")/("S"_1"S"_2)` [From Δ S1AS2]
`"tan" theta = "OP"/"CO"` [From Δ POC]
θ → 0 ∴ sin θ ≅ tan θ
∴ `("S"_2"A")/("S"_1"S"_2) = "OP"/"OC"`
`therefore ("S"_2"A")/"d" = "x"/"D"`
`therefore "S"_2"A" = "x d"/"D"`
or p = `"x" "d"/"D"`
∴ For bright fringe,
`"x d"/"D" = "m" lambda`, where m is an integer
∴ xm = `("m"lambda"D")/"d"`
∴ xm+1 = (m + 1) `(lambda"D")/"d"`
∴ Fringe width β = [(m + 1)-m] `(lambda"D")/"d"`
β = `(lambda"D")/"d"`
APPEARS IN
RELATED QUESTIONS
Using monochromatic light of wavelength λ in Young’s double slit experiment, the eleventh dark fringe is obtained on the screen for a phase difference of ______.
Using analytical method for interference bands, obtain an expression for path difference between two light waves.
Suppose white light falls on a double slit but one slit is covered by a violet filter (allowing λ = 400 nm). Describe the nature of the fringe pattern observed.
A transparent paper (refractive index = 1.45) of thickness 0.02 mm is pasted on one of the slits of a Young's double slit experiment which uses monochromatic light of wavelength 620 nm. How many fringes will cross through the centre if the paper is removed?
In a Young's double slit experiment, \[\lambda = 500\text{ nm, d = 1.0 mm and D = 1.0 m.}\] Find the minimum distance from the central maximum for which the intensity is half of the maximum intensity.
The line-width of a bright fringe is sometimes defined as the separation between the points on the two sides of the central line where the intensity falls to half the maximum. Find the line-width of a bright fringe in a Young's double slit experiment in terms of \[\lambda,\] d and D where the symbols have their usual meanings.
In Young’s double slit experiment, what is the effect on fringe pattern if the slits are brought closer to each other?
How will the interference pattern in Young's double-slit experiment be affected if the screen is moved away from the plane of the slits?
A beam of light consisting of two wavelengths 600 nm and 500 nm is used in Young's double slit experiment. The silt separation is 1.0 mm and the screen is kept 0.60 m away from the plane of the slits. Calculate:
- the distance of the second bright fringe from the central maximum for wavelength 500 nm, and
- the least distance from the central maximum where the bright fringes due to both wavelengths coincide.
In Young's double slit experiment the two slits are 0.6 mm distance apart. Interference pattern is observed on a screen at a distance 80 cm from the slits. The first dark fringe is observed on the screen directly opposite to one of the slits. The wavelength of light will be ______ nm.
