Advertisements
Advertisements
प्रश्न
In Young’s double-slit experiment, show that:
`beta = (lambda "D")/"d"` where the terms have their usual meaning.
उत्तर
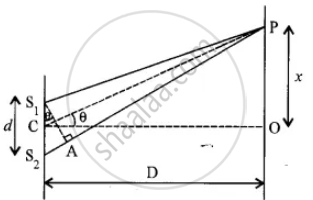
d = Distance between the slits
D = Distance between slit and screen
'P' is the position of mth order bright fringe.
From diagram, the path difference p is
S2P - S1P = S2P - AP
= S2A
`"sin"theta = ("S"_2"A")/("S"_1"S"_2)` [From Δ S1AS2]
`"tan" theta = "OP"/"CO"` [From Δ POC]
θ → 0 ∴ sin θ ≅ tan θ
∴ `("S"_2"A")/("S"_1"S"_2) = "OP"/"OC"`
`therefore ("S"_2"A")/"d" = "x"/"D"`
`therefore "S"_2"A" = "x d"/"D"`
or p = `"x" "d"/"D"`
∴ For bright fringe,
`"x d"/"D" = "m" lambda`, where m is an integer
∴ xm = `("m"lambda"D")/"d"`
∴ xm+1 = (m + 1) `(lambda"D")/"d"`
∴ Fringe width β = [(m + 1)-m] `(lambda"D")/"d"`
β = `(lambda"D")/"d"`
APPEARS IN
संबंधित प्रश्न
In a double-slit experiment using the light of wavelength 600 nm, the angular width of the fringe formed on a distant screen is 0.1°. Find the spacing between the two slits.
Show that the angular width of the first diffraction fringe is half that of the central fringe.
In Young’s experiment, the ratio of intensity at the maxima and minima in an interference
pattern is 36 : 9. What will be the ratio of the intensities of two interfering waves?
The fringes produced in diffraction pattern are of _______.
(A) equal width with same intensity
(B) unequal width with varying intensity
(C) equal intensity\
(D) equal width with varying intensity
In Young's double slit experiment, derive the condition for
(i) constructive interference and
(ii) destructive interference at a point on the screen.
What is the effect on the interference fringes to a Young’s double slit experiment when
(i) the separation between the two slits is decreased?
(ii) the width of a source slit is increased?
(iii) the monochromatic source is replaced by a source of white light?
Justify your answer in each case.
In a Young's double slit experiment, the separation between the slits = 2.0 mm, the wavelength of the light = 600 nm and the distance of the screen from the slits = 2.0 m. If the intensity at the centre of the central maximum is 0.20 W m−2, what will be the intensity at a point 0.5 cm away from this centre along the width of the fringes?
A thin circular ring of mass M and radius R is rotating about its axis with a constant angular velocity ω. Two objects each of mass m are attached gently to the opposite ends of diameter of the ring. The ring will now rotate with an angular velocity:
A slit of width 0.6 mm is illuminated by a beam of light consisting of two wavelengths 600 nm and 480 nm. The diffraction pattern is observed on a screen 1.0 m from the slit. Find:
- The distance of the second bright fringe from the central maximum pertaining to the light of 600 nm.
- The least distance from the central maximum at which bright fringes due to both wavelengths coincide.
- Assertion (A): In Young's double slit experiment all fringes are of equal width.
- Reason (R): The fringe width depends upon the wavelength of light (λ) used, the distance of the screen from the plane of slits (D) and slits separation (d).
