Advertisements
Advertisements
Question
Using analytical method for interference bands, obtain an expression for path difference between two light waves.
Solution
a) Let S1 and S2 be the two coherent monochromatic sources which are separated by short distance d. They emit light waves of wavelength λ
b) Let D = horizontal distance between screen and source
c) Draw S1M and S2N ⊥ AB
OP = perpendicular bisector of slit.
Since S1P = S2P, the path difference between waves reaching P from S1 and S2 is zero, therefore there is a bright point at P.
d) Consider a point Q on the screen which is at a distance x from the central point P on the screen. Light waves from S1 and S2 reach at Q simultaneously by covering path S1Q and S2Q, where they superimpose


h). If x << D and d << D then,
S1Q ≈ S2Q ≈ D
S2Q + S1Q = 2D
∴ Equation (3) becomes,
`S_2Q - S_1Q = (2xd)/(2D)`
`:. S_2Q - S_1Q = (xd)/D`
`:.trianglex = (xd)/D` .........4
Equation (4) gives the path difference of two interfering light waves
APPEARS IN
RELATED QUESTIONS
Derive an expression for path difference in Young’s double slit experiment and obtain the conditions for constructive and destructive interference at a point on the screen.
In Young's double slit experiment, plot a graph showing the variation of fringe width versus the distance of the screen from the plane of the slits keeping other parameters same. What information can one obtain from the slope of the curve?
What is the effect on the fringe width if the distance between the slits is reduced keeping other parameters same?
In Young's double slit experiment, describe briefly how bright and dark fringes are obtained on the screen kept in front of a double slit. Hence obtain the expression for the fringe width.
Using monochromatic light of wavelength λ in Young’s double slit experiment, the eleventh dark fringe is obtained on the screen for a phase difference of ______.
A monochromatic light of wavelength 500 nm is incident normally on a single slit of width 0.2 mm to produce a diffraction pattern. Find the angular width of the central maximum obtained on the screen.
Estimate the number of fringes obtained in Young's double slit experiment with fringe width 0.5 mm, which can be accommodated within the region of total angular spread of the central maximum due to single slit.
If one of two identical slits producing interference in Young’s experiment is covered with glass, so that the light intensity passing through it is reduced to 50%, find the ratio of the maximum and minimum intensity of the fringe in the interference pattern.
In Young’s experiment interference bands were produced on a screen placed at 150 cm from two slits, 0.15 mm apart and illuminated by the light of wavelength 6500 Å. Calculate the fringe width.
Can we perform Young's double slit experiment with sound waves? To get a reasonable "fringe pattern", what should be the order of separation between the slits? How can the bright fringes and the dark fringes be detected in this case?
If the separation between the slits in a Young's double slit experiment is increased, what happens to the fringe-width? If the separation is increased too much, will the fringe pattern remain detectable?
The slits in a Young's double slit experiment have equal width and the source is placed symmetrically with respect to the slits. The intensity at the central fringe is I0. If one of the slits is closed, the intensity at this point will be ____________ .
The separation between the consecutive dark fringes in a Young's double slit experiment is 1.0 mm. The screen is placed at a distance of 2.5m from the slits and the separation between the slits is 1.0 mm. Calculate the wavelength of light used for the experiment.
In a double slit interference experiment, the separation between the slits is 1.0 mm, the wavelength of light used is 5.0 × 10−7 m and the distance of the screen from the slits is 1.0m. (a) Find the distance of the centre of the first minimum from the centre of the central maximum. (b) How many bright fringes are formed in one centimetre width on the screen?
In a Young's double slit experiment, using monochromatic light, the fringe pattern shifts by a certain distance on the screen when a mica sheet of refractive index 1.6 and thickness 1.964 micron (1 micron = 10−6 m) is introduced in the path of one of the interfering waves. The mica sheet is then removed and the distance between the screen and the slits is doubled. It is found that the distance between the successive maxima now is the same as the observed fringe-shift upon the introduction of the mica sheet. Calculate the wavelength of the monochromatic light used in the experiment.
White coherent light (400 nm-700 nm) is sent through the slits of a Young's double slit experiment (see the following figure). The separation between the slits is 0⋅5 mm and the screen is 50 cm away from the slits. There is a hole in the screen at a point 1⋅0 mm away (along the width of the fringes) from the central line. (a) Which wavelength(s) will be absent in the light coming from the hole? (b) Which wavelength(s) will have a strong intensity?
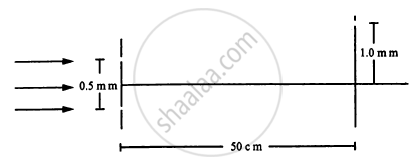
In Young's double slit experiment using monochromatic light of wavelength 600 nm, 5th bright fringe is at a distance of 0·48 mm from the centre of the pattern. If the screen is at a distance of 80 cm from the plane of the two slits, calculate:
(i) Distance between the two slits.
(ii) Fringe width, i.e. fringe separation.
In Young’s double-slit experiment, using monochromatic light, fringes are obtained on a screen placed at some distance from the slits. If the screen is moved by 5 x 10-2 m towards the slits, the change in the fringe width is 3 x 10-5 m. If the distance between the two slits is 10-3 m, calculate the wavelength of the light used.
In Young’s double-slit experiment, show that:
`beta = (lambda "D")/"d"` where the terms have their usual meaning.
"If the slits in Young's double slit experiment are identical, then intensity at any point on the screen may vary between zero and four times to the intensity due to single slit".
Justify the above statement through a relevant mathematical expression.
Young's double slit experiment is made in a liquid. The 10th bright fringe lies in liquid where 6th dark fringe lies in vacuum. The refractive index of the liquid is approximately
The Young's double slit experiment is performed with blue and with green light of wavelengths 4360Å and 5460Å respectively. If x is the distance of 4th maxima from the central one, then:
Why is the diffraction of sound waves more evident in daily experience than that of light wave?
ASSERTION (A): In an interference pattern observed in Young's double slit experiment, if the separation (d) between coherent sources as well as the distance (D) of the screen from the coherent sources both are reduced to 1/3rd, then new fringe width remains the same.
REASON (R): Fringe width is proportional to (d/D).
In Young's double slit experiment using light of wavelength 600 nm, the slit separation is 0.8 mm and the screen is kept 1.6 m from the plane of the slits. Calculate
- the fringe width
- the distance of (a) third minimum and (b) fifth maximum, from the central maximum.
Interference fringes are observed on a screen by illuminating two thin slits 1 mm apart with a light source (λ = 632.8 nm). The distance between the screen and the slits is 100 cm. If a bright fringe is observed on a screen at distance of 1.27 mm from the central bright fringe, then the path difference between the waves, which are reaching this point from the slits is close to :
The central fringe of the interference pattern produced by the light of wavelength 6000 Å is found to shift to the position of the fourth bright fringe after a glass plate of refractive index 1.5 is introduced in the path of one of the beams. The thickness of the glass plate would be ______.
- Assertion (A): In Young's double slit experiment all fringes are of equal width.
- Reason (R): The fringe width depends upon the wavelength of light (λ) used, the distance of the screen from the plane of slits (D) and slits separation (d).
In Young's double slit experiment, show that:
`β = (λ"D")/"d"`
Where the terms have their usual meaning.
