Advertisements
Advertisements
प्रश्न
Show that the fringe pattern on the screen is actually a superposition of slit diffraction from each slit.
उत्तर
The intensity variation in the fringe pattern obtained on a screen in a Young’s double slit experiment corresponds to both single slit diffraction and double slit interference because the two sources are slits of finite width in the double slit experiment.
If a lens is placed in front of the double slits and when one of the slit S1 is closed and the other kept open, a single slit diffraction is formed on the screen. A similar diffraction pattern is obtained on the screen if the slit S1 is kept open and S2 is closed. Both diffraction patterns form on the same position on the screen in the focal plane of the lens. When both slits open simultaneously, the resulting total intensity pattern on the screen is actually the superposition of the single slit diffraction pattern formed by waves from various point sources of each slit and a double slit interference pattern as shown. The actual double slit intensity pattern consists of the interference pattern (solid lines) formed within the diffraction pattern (dotted lines).
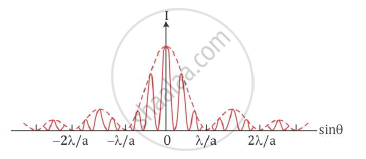
APPEARS IN
संबंधित प्रश्न
(i) In Young's double-slit experiment, deduce the condition for (a) constructive and (b) destructive interferences at a point on the screen. Draw a graph showing variation of intensity in the interference pattern against position 'x' on the screen.
(b) Compare the interference pattern observed in Young's double-slit experiment with single-slit diffraction pattern, pointing out three distinguishing features.
Using analytical method for interference bands, obtain an expression for path difference between two light waves.
In Young’s double slit experiment using monochromatic light of wavelength λ, the intensity of light at a point on the screen where path difference is λ, is K units. Find out the intensity of light at a point where path difference is λ/3.
Find the angular separation between the consecutive bright fringes in a Young's double slit experiment with blue-green light of wavelength 500 nm. The separation between the slits is \[2 \cdot 0 \times {10}^{- 3}m.\]
A Young's double slit apparatus has slits separated by 0⋅28 mm and a screen 48 cm away from the slits. The whole apparatus is immersed in water and the slits are illuminated by red light \[\left( \lambda = 700\text{ nm in vacuum} \right).\] Find the fringe-width of the pattern formed on the screen.
In a Young's double slit experiment, \[\lambda = 500\text{ nm, d = 1.0 mm and D = 1.0 m.}\] Find the minimum distance from the central maximum for which the intensity is half of the maximum intensity.
Draw the intensity distribution as function of phase angle when diffraction of light takes place through coherently illuminated single slit.
Monochromatic green light of wavelength 5 × 10-7 m illuminates a pair of slits 1 mm apart. The separation of bright lines in the interference pattern formed on a screen 2 m away is ______.
In Young's double-slit experiment, the separation between the two slits is d and the distance of the screen from the slits is 1000 d. If the first minima fall at a distance d from the central maximum, obtain the relation between d and λ.
In an interference experiment, a third bright fringe is obtained at a point on the screen with a light of 700 nm. What should be the wavelength of the light source in order to obtain the fifth bright fringe at the same point?
