Advertisements
Advertisements
प्रश्न
In an interference experiment, a third bright fringe is obtained at a point on the screen with a light of 700 nm. What should be the wavelength of the light source in order to obtain the fifth bright fringe at the same point?
विकल्प
420 nm
750 nm
630 nm
500 nm
उत्तर
420 nm
Explanation:
Position of nth bright fringe,
`y_n = (nlambdaD)/d`
Given: λ = 700 nm
∴ `y_3 = (3 xx 700 xx D)/d`
⇒ `y_3 = (2100D)/d`
The 5th bright fringe due to light of wavelength λ' is formed at y3,
∴ y5 = y3
or `(5 xx lambda^'D)/d = (2100 nmD)/d`
⇒ `lambda^' = 2100/5` = 420 nm
APPEARS IN
संबंधित प्रश्न
Show that the fringe pattern on the screen is actually a superposition of slit diffraction from each slit.
In Young's double slit experiment, plot a graph showing the variation of fringe width versus the distance of the screen from the plane of the slits keeping other parameters same. What information can one obtain from the slope of the curve?
How does the fringe width get affected, if the entire experimental apparatus of Young is immersed in water?
In a Young's double slit experiment, using monochromatic light, the fringe pattern shifts by a certain distance on the screen when a mica sheet of refractive index 1.6 and thickness 1.964 micron (1 micron = 10−6 m) is introduced in the path of one of the interfering waves. The mica sheet is then removed and the distance between the screen and the slits is doubled. It is found that the distance between the successive maxima now is the same as the observed fringe-shift upon the introduction of the mica sheet. Calculate the wavelength of the monochromatic light used in the experiment.
A thin paper of thickness 0.02 mm having a refractive index 1.45 is pasted across one of the slits in a Young's double slit experiment. The paper transmits 4/9 of the light energy falling on it. (a) Find the ratio of the maximum intensity to the minimum intensity in the fringe pattern. (b) How many fringes will cross through the centre if an identical paper piece is pasted on the other slit also? The wavelength of the light used is 600 nm.
A Young's double slit apparatus has slits separated by 0⋅28 mm and a screen 48 cm away from the slits. The whole apparatus is immersed in water and the slits are illuminated by red light \[\left( \lambda = 700\text{ nm in vacuum} \right).\] Find the fringe-width of the pattern formed on the screen.
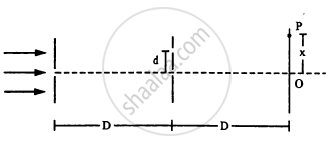
Consider the arrangement shown in the figure. The distance D is large compared to the separation d between the slits.
- Find the minimum value of d so that there is a dark fringe at O.
- Suppose d has this value. Find the distance x at which the next bright fringe is formed.
- Find the fringe-width.
In Young’s double-slit experiment, using monochromatic light, fringes are obtained on a screen placed at some distance from the slits. If the screen is moved by 5 x 10-2 m towards the slits, the change in the fringe width is 3 x 10-5 m. If the distance between the two slits is 10-3 m, calculate the wavelength of the light used.
When a beam of light is used to determine the position of an object, the maximum accuracy is achieved, if the light is ______.
Two beams of light having intensities I and 41 interfere to produce a fringe pattern on a screen. The phase difference between the two beams are π/2 and π/3 at points A and B respectively. The difference between the resultant intensities at the two points is xl. The value of x will be ______.
