Advertisements
Advertisements
प्रश्न
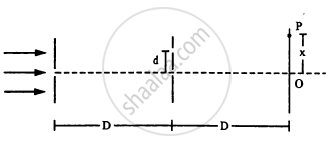
Consider the arrangement shown in the figure. The distance D is large compared to the separation d between the slits.
- Find the minimum value of d so that there is a dark fringe at O.
- Suppose d has this value. Find the distance x at which the next bright fringe is formed.
- Find the fringe-width.
उत्तर
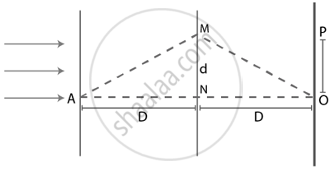
From the figure,
Δx = AMO − ANO
Here AM = MO = √[D2 + d2] AND AN = NO = D
=> Δx = 2(AM − AN) = 2 {√[D2 + d2] - D}
For minima at O,
2 {√[D2 + d2] − D} = (n +(1/2)) λ
Solving above equation for d, we get
d = √[Dλ/2]
(b) width of the dark fringe = w = Dλ/d
Now, the location x is given by
x = Dλ/[2√(Dλ/2)]
=> x = d
(c) As x = w/2
=> w = 2x = 2d
APPEARS IN
संबंधित प्रश्न
In Young's double slit experiment, describe briefly how bright and dark fringes are obtained on the screen kept in front of a double slit. Hence obtain the expression for the fringe width.
In a double-slit experiment the angular width of a fringe is found to be 0.2° on a screen placed 1 m away. The wavelength of light used is 600 nm. What will be the angular width of the fringe if the entire experimental apparatus is immersed in water? Take refractive index of water to be 4/3.
The fringes produced in diffraction pattern are of _______.
(A) equal width with same intensity
(B) unequal width with varying intensity
(C) equal intensity\
(D) equal width with varying intensity
How does the fringe width get affected, if the entire experimental apparatus of Young is immersed in water?
In Young’s experiment interference bands were produced on a screen placed at 150 cm from two slits, 0.15 mm apart and illuminated by the light of wavelength 6500 Å. Calculate the fringe width.
Two coherent sources of light having intensity ratio 81 : 1 produce interference fringes. Calculate the ratio of intensities at the maxima and minima in the interference pattern.
Can we perform Young's double slit experiment with sound waves? To get a reasonable "fringe pattern", what should be the order of separation between the slits? How can the bright fringes and the dark fringes be detected in this case?
If the source of light used in a Young's double slit experiment is changed from red to violet, ___________ .
In a double slit interference experiment, the separation between the slits is 1.0 mm, the wavelength of light used is 5.0 × 10−7 m and the distance of the screen from the slits is 1.0m. (a) Find the distance of the centre of the first minimum from the centre of the central maximum. (b) How many bright fringes are formed in one centimetre width on the screen?
White light is used in a Young's double slit experiment. Find the minimum order of the violet fringe \[\left( \lambda = 400\text{ nm} \right)\] which overlaps with a red fringe \[\left( \lambda = 700\text{ nm} \right).\]
A plate of thickness t made of a material of refractive index µ is placed in front of one of the slits in a double slit experiment. (a) Find the change in the optical path due to introduction of the plate. (b) What should be the minimum thickness t which will make the intensity at the centre of the fringe pattern zero? Wavelength of the light used is \[\lambda.\] Neglect any absorption of light in the plate.
A thin paper of thickness 0.02 mm having a refractive index 1.45 is pasted across one of the slits in a Young's double slit experiment. The paper transmits 4/9 of the light energy falling on it. (a) Find the ratio of the maximum intensity to the minimum intensity in the fringe pattern. (b) How many fringes will cross through the centre if an identical paper piece is pasted on the other slit also? The wavelength of the light used is 600 nm.
"If the slits in Young's double slit experiment are identical, then intensity at any point on the screen may vary between zero and four times to the intensity due to single slit".
Justify the above statement through a relevant mathematical expression.
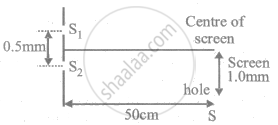
In Young's double slit experiment shown in figure S1 and S2 are coherent sources and S is the screen having a hole at a point 1.0 mm away from the central line. White light (400 to 700 nm) is sent through the slits. Which wavelength passing through the hole has strong intensity?
ASSERTION (A): In an interference pattern observed in Young's double slit experiment, if the separation (d) between coherent sources as well as the distance (D) of the screen from the coherent sources both are reduced to 1/3rd, then new fringe width remains the same.
REASON (R): Fringe width is proportional to (d/D).
In a Young's double slit experiment, the width of the one of the slit is three times the other slit. The amplitude of the light coming from a slit is proportional to the slit- width. Find the ratio of the maximum to the minimum intensity in the interference pattern.
In Young's double-slit experiment, the separation between the two slits is d and the distance of the screen from the slits is 1000 d. If the first minima fall at a distance d from the central maximum, obtain the relation between d and λ.
In an interference experiment, a third bright fringe is obtained at a point on the screen with a light of 700 nm. What should be the wavelength of the light source in order to obtain the fifth bright fringe at the same point?
