Advertisements
Advertisements
प्रश्न
In Young’s double slit experiment using monochromatic light of wavelength λ, the intensity of light at a point on the screen where path difference is λ, is K units. Find out the intensity of light at a point where path difference is λ/3.
उत्तर
We know
Phase difference `= ((2pi)/lambda) xx` path difference
At path difference λ
Phase difference ,`phi = (2pi)/lambda xx lambda = 2pi`
Intensity, `I = 4I_0 cos^2 phi/2`
or ,` K = 4I_0 cos^2 (2pi)/2` [given I = K at path difference λ]
or, `K = 4I_0`
or ,`I_0 = K/4`
Now, at path difference `= lambda/3`
`phi' = (2pi)/lambda xx lambda/3 = (2pi)/3`
Intensity , `I' =4I_0 cos^2 1/2 ((2pi)/3)`
0r, `I' = 4 xx K/4 cos^2 pi/3`
`I'=K/4`
APPEARS IN
संबंधित प्रश्न
Show that the angular width of the first diffraction fringe is half that of the central fringe.
If one of two identical slits producing interference in Young’s experiment is covered with glass, so that the light intensity passing through it is reduced to 50%, find the ratio of the maximum and minimum intensity of the fringe in the interference pattern.
If the separation between the slits in a Young's double slit experiment is increased, what happens to the fringe-width? If the separation is increased too much, will the fringe pattern remain detectable?
Consider the arrangement shown in the figure. The distance D is large compared to the separation d between the slits.
- Find the minimum value of d so that there is a dark fringe at O.
- Suppose d has this value. Find the distance x at which the next bright fringe is formed.
- Find the fringe-width.
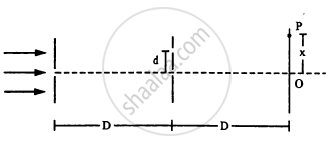
In a Young's double slit experiment, \[\lambda = 500\text{ nm, d = 1.0 mm and D = 1.0 m.}\] Find the minimum distance from the central maximum for which the intensity is half of the maximum intensity.
In Young’s double-slit experiment, using monochromatic light, fringes are obtained on a screen placed at some distance from the slits. If the screen is moved by 5 x 10-2 m towards the slits, the change in the fringe width is 3 x 10-5 m. If the distance between the two slits is 10-3 m, calculate the wavelength of the light used.
An unpolarised beam of intensity 2a2 passes through a thin polaroid. Assuming zero absorption in the polaroid, the intensity of emergent plane polarised light will be
ASSERTION (A): In an interference pattern observed in Young's double slit experiment, if the separation (d) between coherent sources as well as the distance (D) of the screen from the coherent sources both are reduced to 1/3rd, then new fringe width remains the same.
REASON (R): Fringe width is proportional to (d/D).
How will the interference pattern in Young's double-slit experiment be affected if the phase difference between the light waves emanating from the two slits S1 and S2 changes from 0 to π and remains constant?
Two beams of light having intensities I and 41 interfere to produce a fringe pattern on a screen. The phase difference between the two beams are π/2 and π/3 at points A and B respectively. The difference between the resultant intensities at the two points is xl. The value of x will be ______.
