Advertisements
Advertisements
प्रश्न
Draw the intensity distribution as function of phase angle when diffraction of light takes place through coherently illuminated single slit.
उत्तर
Intensity distribution as function of phase angle, when diffraction of light takes place through coherently illuminated single slit.
The Intensity pattern on the screen is shown in the given figure.
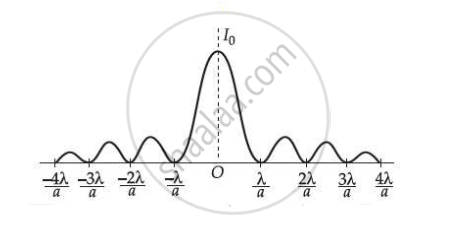
Width of central maximum = `(2"D"λ)/"a"`
APPEARS IN
संबंधित प्रश्न
In Young's double slit experiment, describe briefly how bright and dark fringes are obtained on the screen kept in front of a double slit. Hence obtain the expression for the fringe width.
A beam of light consisting of two wavelengths, 650 nm and 520 nm, is used to obtain interference fringes in a Young’s double-slit experiment.
Find the distance of the third bright fringe on the screen from the central maximum for wavelength 650 nm.
Explain two features to distinguish between the interference pattern in Young's double slit experiment with the diffraction pattern obtained due to a single slit.
In Young’s double slit experiment using monochromatic light of wavelength λ, the intensity of light at a point on the screen where path difference is λ, is K units. Find out the intensity of light at a point where path difference is λ/3.
In a Young's double slit experiment, using monochromatic light, the fringe pattern shifts by a certain distance on the screen when a mica sheet of refractive index 1.6 and thickness 1.964 micron (1 micron = 10−6 m) is introduced in the path of one of the interfering waves. The mica sheet is then removed and the distance between the screen and the slits is doubled. It is found that the distance between the successive maxima now is the same as the observed fringe-shift upon the introduction of the mica sheet. Calculate the wavelength of the monochromatic light used in the experiment.
A parallel beam of monochromatic light is used in a Young's double slit experiment. The slits are separated by a distance d and the screen is placed parallel to the plane of the slits. Slow that if the incident beam makes an angle \[\theta = \sin^{- 1} \left( \frac{\lambda}{2d} \right)\] with the normal to the plane of the slits, there will be a dark fringe at the centre P0 of the pattern.
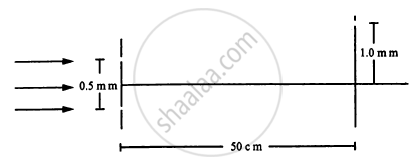
White coherent light (400 nm-700 nm) is sent through the slits of a Young's double slit experiment (see the following figure). The separation between the slits is 0⋅5 mm and the screen is 50 cm away from the slits. There is a hole in the screen at a point 1⋅0 mm away (along the width of the fringes) from the central line. (a) Which wavelength(s) will be absent in the light coming from the hole? (b) Which wavelength(s) will have a strong intensity?
In a Young’s double slit experiment, the source is white light. One of the holes is covered by a red filter and another by a blue filter. In this case ______.
The maximum number of possible interference maxima for slit-separation equal to twice the wavelength in Young's double-slit experiment is ______.
In an interference experiment, a third bright fringe is obtained at a point on the screen with a light of 700 nm. What should be the wavelength of the light source in order to obtain the fifth bright fringe at the same point?
