Advertisements
Advertisements
Question
Two coherent point sources S1 and S2, vibrating in phase, emit light of wavelength \[\lambda.\] The separation between the sources is \[2\lambda.\] Consider a line passing through S2 and perpendicular to the line S1 S2. What is the smallest distance from S2 where a minimum intensity occurs?
Solution

Let P be the point of minimum intensity.
For minimum intensity at point P,
\[S_1 P - S_2 P = x = \left( 2n + 1 \right) \frac{\lambda}{2}\]
Thus, we get
\[\sqrt{Z^2 + \left( 2\lambda \right)^2} - Z = \left( 2n + 1 \right) \frac{\lambda}{2}\]
\[ \Rightarrow Z^2 + 4 \lambda^2 = Z^2 \left( 2n + 1 \right)^2 \frac{\lambda^2}{4} + 2Z \left( 2n + 1 \right) \frac{\lambda}{2}\]
\[ \Rightarrow Z = \frac{4 \lambda^2 - \left( 2n + 1 \right) 2 \lambda^2 /4}{\left( 2n + 1 \right) \lambda}\]
\[ = \frac{16 \lambda^2 - \left( 2n + 1 \right)}{4 \left( 2n + 1 \right) \lambda}............(1)\]
\[\text{When }n = 0, Z = \frac{15\lambda}{4}\]
\[ n = - 1, Z = \frac{- 15\lambda}{4}\]
\[ n = 1, Z = \frac{7\lambda}{12}\]
\[ n = 2 , Z = \frac{- 9\lambda}{20}\]
Thus, \[Z = \frac{7\lambda}{12}\] is the smallest distance for which there will be minimum intensity.
APPEARS IN
RELATED QUESTIONS
When a tiny circular obstacle is placed in the path of light from a distant source, a bright spot is seen at the centre of the shadow of the obstacle. Explain why?
Two sources are called coherent if they produce waves ______________ .
Two coherent sources of different intensities send waves which interfere. The ratio of maximum intensity to the minimum intensity is 25. The intensities of the sources are in the ratio ______.
Two sources of light are coherent if they have ______.
Two source S1 and S2 of intensity I1 and I2 are placed in front of a screen [Figure (a)]. The pattern of intensity distribution seen in the central portion is given by Figure (b).
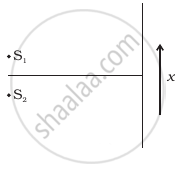 (a) |
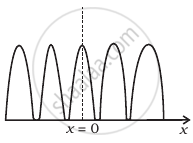 (b) |
- S1 and S2 have the same intensities.
- S1 and S2 have a constant phase difference.
- S1 and S2 have the same phase.
- S1 and S2 have the same wavelength.
n identical waves each of intensity I0 interfere with each other. The ratio of maximum intensities if the interference is (i) coherent and (ii) incoherent is ______.
