Advertisements
Advertisements
Question
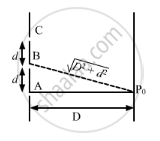
The following figure shows three equidistant slits being illuminated by a monochromatic parallel beam of light. Let \[B P_0 - A P_0 = \lambda/3\text{ and }D > > \lambda.\] (a) Show that in this case \[d = \sqrt{2\lambda D/3}.\] (b) Show that the intensity at P0 is three times the intensity due to any of the three slits individually.
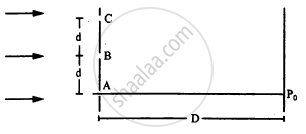
Solution
(a) Given:-
Wavelength of light = \[\lambda\]
Path difference of wave fronts reaching from A and B is given by
\[∆ x_B = {BP}_0 - {AP}_0 = \frac{\lambda}{3}\]
\[ \Rightarrow \sqrt{D^2 + d^2} - D = \frac{\lambda}{3}\]
\[ \Rightarrow D^2 + d^2 = D^2 + \frac{\lambda^2}{9} + \frac{2\lambda D}{3}\]
We will neglect the term \[\frac{\lambda^2}{9},\] as it has a very small value.
\[\therefore d = \sqrt{\frac{\left( 2\lambda D \right)}{3}}\]
(b) To calculating the intensity at P0, consider the interference of light waves coming from all the three slits.
Path difference of the wave fronts reaching from A and C is given by
\[{CP}_0 - {AP}_0 = \sqrt{D^2 + \left( 2d \right)^2} - D\]
\[ = \sqrt{D^2 + \frac{8\lambda D}{3}} - D ........\left(\text{Using the value of d from part a} \right)\]
\[ = D \left\{ 1 + \frac{8\lambda}{3D} \right\}^\frac{1}{2} - D\]
Expanding the value using binomial theorem and neglectingthe higher order terms, we get
\[ D\left\{ 1 + \frac{1}{2} \times \frac{8\lambda}{3D} + . . . \right\} - D\]
\[{CP}_0 - {AP}_0 = \frac{4\lambda}{3}\]
So, the corresponding phase difference between the wave fronts from A and C is given by
\[\phi_c = \frac{2\pi ∆ x_C}{\lambda} = \frac{2\pi \times 4\lambda}{3\lambda}\]
\[ \Rightarrow \phi_c = \frac{8\pi}{3}\text{ or }\left( 2\pi + \frac{2\pi}{3} \right)\]
\[ \Rightarrow \phi_c = \frac{2\pi}{3}...........(1)\]
Again, \[\phi_B = \frac{2\pi ∆ x_B}{\lambda}\]
\[ \Rightarrow \phi_B = \frac{2\pi\lambda}{3\lambda} = \frac{2\pi}{3}..........(2)\]
So, it can be said that light from B and C are in the same phase, as they have the same phase difference with respect to A.
Amplitude of wave reaching P0 is given by
\[A = \sqrt{\left( 2a \right)^2 + a^2 + 2a \times a\cos\left( \frac{2\pi}{3} \right)}\]
\[ = \sqrt{4 a^2 + a^2 + 2 a^2 \sqrt{3}}\]
\[ \therefore l_{po} = K \left( \sqrt{3} r \right)^2 = 3 K r^2 = 3l\]
Here, I is the intensity due to the individual slits and Ipo is the total intensity at P0.
Thus, the resulting amplitude is three times the intensity due to the individual slits.
APPEARS IN
RELATED QUESTIONS
When monochromatic light is incident on a surface separating two media, the reflected and refracted light both have the same frequency as the incident frequency.
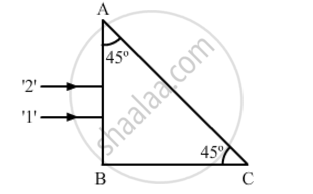
Two monochromatic rays of light are incident normally on the face AB of an isosceles right-angled prism ABC. The refractive indices of the glass prism for the two rays '1' and '2' are respectively 1.3 and 1.5. Trace the path of these rays after entering the prism.
What kind of fringes do you expect to observe if white light is used instead of monochromatic light?
A monochromatic ray of light falls on a regular prism. What is the relation between the angle of incidence and angle of emergence in the case of minimum deviation?
Monochromatic light of frequency 5.0 × 1014 Hz is produced by a laser. The power emitted is 3.0 × 10–3 W. Estimate the number of photons emitted per second on an average by the source ?
Obtain the conditions for the bright and dark fringes in diffraction pattern due to a single narrow slit illuminated by a monochromatic source.
Explain clearly why the secondary maxima go on becoming weaker with increasing.
If a monochromatic source of light is replaced by white light, what change would you observe in the diffraction pattern?
Consider the situation shown in the figure. The two slits S1 and S2 placed symmetrically around the central line are illuminated by a monochromatic light of wavelength λ. The separation between the slits is d. The light transmitted by the slits falls on a screen ∑1placed at a distance D from the slits. The slit S3 is at the central line and the slit S4 is at a distance z from S3. Another screen ∑2 is placed a further distance D away from ∑1.Find the ratio of the maximum to minimum intensity observed on ∑2 if z is equal to
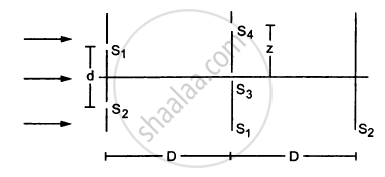
(a) \[z = \frac{\lambda D}{2d}\]
(b) \[\frac{\lambda D}{d}\]
(c) \[\frac{\lambda D}{4d}\]
Can the interference pattern be produced by two independent monochromatic sources of light? Explain.
Monochromatic light of wavelength 650 nm falls normally on a slit of width 1.3 x 10-4 cm and the resulting Fraunhofer diffraction is obtained on a screen. Find the angular width of the . central maxima.
Answer the following question.
In the diffraction due to a single slit experiment, the aperture of the slit is 3 mm. If monochromatic light of wavelength 620 nm is incident normally on the slit, calculate the separation between the first order minima and the 3rd order maxima on one side of the screen. The distance between the slit and the screen is 1.5 m.
For constructive interference to take place between two monochromatic light waves of wavelength λ, the path difference should be ______.
Assertion(A): The photoelectrons produced by a monochromatic light beam incident on a metal surface have a spread in their kinetic energies.
Reason(R): The energy of electrons emitted from inside the metal surface, is lost in collision with the other atoms in the metal.
Monochromatic light of wavelength 600 nm is incident from the air on a water surface. The refractive index of water is 1.33. Find the
- wavelength,
- frequency and
- speed, of reflected and refracted light.
A ray of monochromatic light propagating in the air is incident on the surface of the water. Which of the following will be the same for the reflected and refracted rays?
Monochromatic light of wavelength 396 nm is incident on the surface of a metal whose work function is 1.125 eV. Calculate:
- the energy of an incident photon in eV.
- the maximum kinetic energy of photoelectrons in eV.
The Figure below shows a ray of monochromatic light LM incident on the first surface AB of a regular (equilateral) glass prism ABC. The emergent ray grazes the adjacent surface AC. Calculate the angle of incidence. (Refractive Index of glass = 1.5)

