Advertisements
Advertisements
प्रश्न
A plate of thickness t made of a material of refractive index µ is placed in front of one of the slits in a double slit experiment. (a) Find the change in the optical path due to introduction of the plate. (b) What should be the minimum thickness t which will make the intensity at the centre of the fringe pattern zero? Wavelength of the light used is \[\lambda.\] Neglect any absorption of light in the plate.
उत्तर
Given:-
Refractive index of the plate is μ.
The thickness of the plate is t.
Wavelength of the light is λ.
(a)
When the plate is placed in front of the slit, then the optical path difference is given by \[\left( \mu - 1 \right)t\]
(b) For zero intensity at the centre of the fringe pattern, there should be distractive interference at the centre.
So, the optical path difference should be = \[\frac{\lambda}{2}\]
\[i . e . \left( \mu - 1 \right) t = \frac{\lambda}{2}\]
\[ \Rightarrow t = \frac{\lambda}{2 \left( \mu - 1 \right)}\]
APPEARS IN
संबंधित प्रश्न
In Young' s experiment the ratio of intensity at the maxima and minima . in the interference pattern is 36 : 16. What is the ratio of the widths of the two slits?
In Young's double slit experiment, describe briefly how bright and dark fringes are obtained on the screen kept in front of a double slit. Hence obtain the expression for the fringe width.
Using monochromatic light of wavelength λ in Young’s double slit experiment, the eleventh dark fringe is obtained on the screen for a phase difference of ______.
A beam of light consisting of two wavelengths, 650 nm and 520 nm, is used to obtain interference fringes in a Young’s double-slit experiment.
What is the least distance from the central maximum where the bright fringes due to both the wavelengths coincide?
In Young’s experiment, the ratio of intensity at the maxima and minima in an interference
pattern is 36 : 9. What will be the ratio of the intensities of two interfering waves?
The fringes produced in diffraction pattern are of _______.
(A) equal width with same intensity
(B) unequal width with varying intensity
(C) equal intensity\
(D) equal width with varying intensity
In Young’s double slit experiment using monochromatic light of wavelength λ, the intensity of light at a point on the screen where path difference is λ, is K units. Find out the intensity of light at a point where path difference is λ/3.
Two polaroids ‘A’ and ‘B’ are kept in crossed position. How should a third polaroid ‘C’ be placed between them so that the intensity of polarized light transmitted by polaroid B reduces to 1/8th of the intensity of unpolarized light incident on A?
Suppose white light falls on a double slit but one slit is covered by a violet filter (allowing λ = 400 nm). Describe the nature of the fringe pattern observed.
If Young's double slit experiment is performed in water, _________________ .
The separation between the consecutive dark fringes in a Young's double slit experiment is 1.0 mm. The screen is placed at a distance of 2.5m from the slits and the separation between the slits is 1.0 mm. Calculate the wavelength of light used for the experiment.
In a Young's double slit experiment, two narrow vertical slits placed 0.800 mm apart are illuminated by the same source of yellow light of wavelength 589 nm. How far are the adjacent bright bands in the interference pattern observed on a screen 2.00 m away?
A mica strip and a polystyrene strip are fitted on the two slits of a double slit apparatus. The thickness of the strips is 0.50 mm and the separation between the slits is 0.12 cm. The refractive index of mica and polystyrene are 1.58 and 1.55, respectively, for the light of wavelength 590 nm which is used in the experiment. The interference is observed on a screen at a distance one metre away. (a) What would be the fringe-width? (b) At what distance from the centre will the first maximum be located?
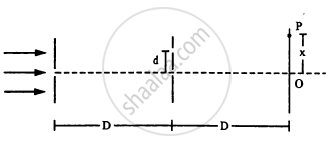
Consider the arrangement shown in the figure. The distance D is large compared to the separation d between the slits.
- Find the minimum value of d so that there is a dark fringe at O.
- Suppose d has this value. Find the distance x at which the next bright fringe is formed.
- Find the fringe-width.
When a beam of light is used to determine the position of an object, the maximum accuracy is achieved, if the light is ______.
Two slits in Young's interference experiment have width in the ratio 1 : 2. The ratio of intensity at the maxima and minima in their interference is ______.
The force required to double the length of a steel wire of area 1 cm2, if its Young's modulus Y= 2 × 1011/m2 is:
How will the interference pattern in Young's double-slit experiment be affected if the phase difference between the light waves emanating from the two slits S1 and S2 changes from 0 to π and remains constant?
The central fringe of the interference pattern produced by the light of wavelength 6000 Å is found to shift to the position of the fourth bright fringe after a glass plate of refractive index 1.5 is introduced in the path of one of the beams. The thickness of the glass plate would be ______.
