Advertisements
Advertisements
प्रश्न
The separation between the consecutive dark fringes in a Young's double slit experiment is 1.0 mm. The screen is placed at a distance of 2.5m from the slits and the separation between the slits is 1.0 mm. Calculate the wavelength of light used for the experiment.
उत्तर
Given:-
Separation between consecutive dark fringes = fringe width (β) = 1 mm = 10−3 m
Distance between screen and slit (D) = 2.5 m
The separation between slits (d) = 1 mm = 10−3 m
Let the wavelength of the light used in experiment be λ.
We know that
\[\beta = \frac{\lambda D}{d}\]
\[{10}^{- 3} m = \frac{2 . 5 \times \lambda}{{10}^{- 3}}\]
\[ \Rightarrow \lambda = \frac{1}{2 . 5} {10}^{- 6} m\]
\[= 4 \times {10}^{- 7} m = 400 \text{ nm}\]
Hence, the wavelength of light used for the experiment is 400 nm.
APPEARS IN
संबंधित प्रश्न
Using monochromatic light of wavelength λ in Young’s double slit experiment, the eleventh dark fringe is obtained on the screen for a phase difference of ______.
A beam of light consisting of two wavelengths, 650 nm and 520 nm, is used to obtain interference fringes in a Young’s double-slit experiment.
Find the distance of the third bright fringe on the screen from the central maximum for wavelength 650 nm.
Explain two features to distinguish between the interference pattern in Young's double slit experiment with the diffraction pattern obtained due to a single slit.
In Young's double slit experiment, derive the condition for
(i) constructive interference and
(ii) destructive interference at a point on the screen.
What is the effect on the interference fringes to a Young’s double slit experiment when
(i) the separation between the two slits is decreased?
(ii) the width of a source slit is increased?
(iii) the monochromatic source is replaced by a source of white light?
Justify your answer in each case.
Can we perform Young's double slit experiment with sound waves? To get a reasonable "fringe pattern", what should be the order of separation between the slits? How can the bright fringes and the dark fringes be detected in this case?
A plate of thickness t made of a material of refractive index µ is placed in front of one of the slits in a double slit experiment. (a) Find the change in the optical path due to introduction of the plate. (b) What should be the minimum thickness t which will make the intensity at the centre of the fringe pattern zero? Wavelength of the light used is \[\lambda.\] Neglect any absorption of light in the plate.
A transparent paper (refractive index = 1.45) of thickness 0.02 mm is pasted on one of the slits of a Young's double slit experiment which uses monochromatic light of wavelength 620 nm. How many fringes will cross through the centre if the paper is removed?
In a Young's double slit experiment, using monochromatic light, the fringe pattern shifts by a certain distance on the screen when a mica sheet of refractive index 1.6 and thickness 1.964 micron (1 micron = 10−6 m) is introduced in the path of one of the interfering waves. The mica sheet is then removed and the distance between the screen and the slits is doubled. It is found that the distance between the successive maxima now is the same as the observed fringe-shift upon the introduction of the mica sheet. Calculate the wavelength of the monochromatic light used in the experiment.
A thin paper of thickness 0.02 mm having a refractive index 1.45 is pasted across one of the slits in a Young's double slit experiment. The paper transmits 4/9 of the light energy falling on it. (a) Find the ratio of the maximum intensity to the minimum intensity in the fringe pattern. (b) How many fringes will cross through the centre if an identical paper piece is pasted on the other slit also? The wavelength of the light used is 600 nm.
In a Young's double slit experiment, \[\lambda = 500\text{ nm, d = 1.0 mm and D = 1.0 m.}\] Find the minimum distance from the central maximum for which the intensity is half of the maximum intensity.
The line-width of a bright fringe is sometimes defined as the separation between the points on the two sides of the central line where the intensity falls to half the maximum. Find the line-width of a bright fringe in a Young's double slit experiment in terms of \[\lambda,\] d and D where the symbols have their usual meanings.
How is the fringe width of an interference pattern in Young's double-slit experiment affected if the two slits are brought closer to each other?
In Young's double-slit experiment, the two slits are separated by a distance of 1.5 mm, and the screen is placed 1 m away from the plane of the slits. A beam of light consisting of two wavelengths of 650 nm and 520 nm is used to obtain interference fringes.
Find the distance of the third bright fringe for λ = 520 nm on the screen from the central maximum.
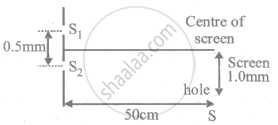
In Young's double slit experiment shown in figure S1 and S2 are coherent sources and S is the screen having a hole at a point 1.0 mm away from the central line. White light (400 to 700 nm) is sent through the slits. Which wavelength passing through the hole has strong intensity?
In a Young’s double slit experiment, the path difference at a certain point on the screen between two interfering waves is `1/8`th of the wavelength. The ratio of intensity at this point to that at the centre of a bright fringe is close to ______.
Monochromatic green light of wavelength 5 × 10-7 m illuminates a pair of slits 1 mm apart. The separation of bright lines in the interference pattern formed on a screen 2 m away is ______.
The maximum number of possible interference maxima for slit-separation equal to twice the wavelength in Young's double-slit experiment is ______.
In Young’s double slit experiment, how is interference pattern affected when the following changes are made:
- Slits are brought closer to each other.
- Screen is moved away from the slits.
- Red coloured light is replaced with blue coloured light.
