Advertisements
Advertisements
प्रश्न
In Young's double slit experiment, derive the condition for
(i) constructive interference and
(ii) destructive interference at a point on the screen.
उत्तर
Young’s double slit experiment: Consider two narrow rectangular slits S1 and S2 placed perpendicular to the plane of paper. Slit S is placed on the perpendicular bisector of S1S2 and is illuminated with monochromatic light.
The slits are separated by a small distance d. A screen is placed at a distance D from S1, S2.
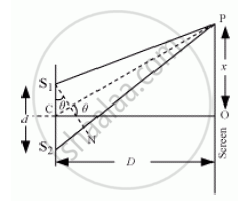
Consider a point P on the screen at distance x from O.
The path difference between the waves reaching P from S1 and S2 is:
P = S2P − S1P
Draw S1N perpendicular to S2P. Then,
P = S2P − S1P = S2P − NP = S2N
From right-angled
`DeltaS_1S^2N=(S_2N)/(S_2S_1) = sintheta`
`therefore P =S_2N=S_2S_1sintheta = d sintheta`
From ΔCOP,
When θ is small,
`sintheta≈theta≈tantheta = x/D`
`therefore P=(xd)/D`
For constructive interference,
`(xd)/D =nlambda,n=0,1,2,3,.....`
Position of nth bright fringe, `x_n = (nDlambda)/d =0,(Dlambda)/d,(2Dlambda)/d,(3Dlambda)/d,.......`
When n = 0, xn = 0, central bright fringe is formed at O.
For destructive interference,
`(xd)/D = (2n +1)lambda/2`
`or x_n = (2_n +1) (lambdaD)/(2d) = 1/2(lambdaD)/d,3/2(lambdaD)/d,5/2(lambdaD)/d,......`
Thus, alternate bright and dark fringes are formed on the screen.
संबंधित प्रश्न
The intensity at the central maxima in Young’s double slit experiment is I0. Find out the intensity at a point where the path difference is` lambda/6,lambda/4 and lambda/3.`
In young’s double slit experiment, deduce the conditions for obtaining constructive and destructive interference fringes. Hence, deduce the expression for the fringe width.
A beam of light consisting of two wavelengths, 650 nm and 520 nm, is used to obtain interference fringes in a Young’s double-slit experiment.
Find the distance of the third bright fringe on the screen from the central maximum for wavelength 650 nm.
In Young’s double slit experiment to produce interference pattern, obtain the conditions for constructive and destructive interference. Hence deduce the expression for the fringe width.
In Young’s experiment interference bands were produced on a screen placed at 150 cm from two slits, 0.15 mm apart and illuminated by the light of wavelength 6500 Å. Calculate the fringe width.
In a double slit interference experiment, the separation between the slits is 1.0 mm, the wavelength of light used is 5.0 × 10−7 m and the distance of the screen from the slits is 1.0m. (a) Find the distance of the centre of the first minimum from the centre of the central maximum. (b) How many bright fringes are formed in one centimetre width on the screen?
A plate of thickness t made of a material of refractive index µ is placed in front of one of the slits in a double slit experiment. (a) Find the change in the optical path due to introduction of the plate. (b) What should be the minimum thickness t which will make the intensity at the centre of the fringe pattern zero? Wavelength of the light used is \[\lambda.\] Neglect any absorption of light in the plate.
A transparent paper (refractive index = 1.45) of thickness 0.02 mm is pasted on one of the slits of a Young's double slit experiment which uses monochromatic light of wavelength 620 nm. How many fringes will cross through the centre if the paper is removed?
In Young's double slit experiment the slits are 0.589 mm apart and the interference is observed on a screen placed at a distance of 100 cm from the slits. It is found that the 9th bright fringe is at a distance of 7.5 mm from the dark fringe which is second from the center of the fringe pattern. Find the wavelength of the light used.
Using Young’s double slit experiment, a monochromatic light of wavelength 5000Å produces fringes of fringe width 0.5 mm. If another monochromatic light of wavelength 6000Å is used and the separation between the slits is doubled, then the new fringe width will be ______.
