Advertisements
Advertisements
प्रश्न
In Young’s experiment interference bands were produced on a screen placed at 150 cm from two slits, 0.15 mm apart and illuminated by the light of wavelength 6500 Å. Calculate the fringe width.
उत्तर
Given:
D = 150 cm = 1.5 m,
d = 0.15 mm = 1.5 x 10-4 m,
λ = 6500 Å = 6.5 x 10-7 m
To find:
Fringe width ( X )
Formula:
X = `"λD"/"d"`
Calculation:
From formula,
X = `[6.5 xx 10^-7 xx 1.5]/[1.5 xx 10^4]`
X = 6.5 x 10-3 m
X = 6.5 mm
The fringe width is 6.5 mm
APPEARS IN
संबंधित प्रश्न
In Young' s experiment the ratio of intensity at the maxima and minima . in the interference pattern is 36 : 16. What is the ratio of the widths of the two slits?
The intensity at the central maxima in Young’s double slit experiment is I0. Find out the intensity at a point where the path difference is` lambda/6,lambda/4 and lambda/3.`
In a double-slit experiment using the light of wavelength 600 nm, the angular width of the fringe formed on a distant screen is 0.1°. Find the spacing between the two slits.
Show that the angular width of the first diffraction fringe is half that of the central fringe.
In Young's double slit experiment, using monochromatic light of wavelength λ, the intensity of light at a point on the screen where path difference is λ, is K units. Find out the intensity of light at a point where path difference is `λ/3`.
In a Young’s double-slit experiment, the slits are separated by 0.28 mm and the screen is placed 1.4 m away. The distance between the central bright fringe and the fourth bright fringe is measured to be 1.2 cm. Determine the wavelength of light used in the experiment.
In a double-slit experiment the angular width of a fringe is found to be 0.2° on a screen placed 1 m away. The wavelength of light used is 600 nm. What will be the angular width of the fringe if the entire experimental apparatus is immersed in water? Take refractive index of water to be 4/3.
In Young’s experiment, the ratio of intensity at the maxima and minima in an interference
pattern is 36 : 9. What will be the ratio of the intensities of two interfering waves?
Write three characteristic features to distinguish between the interference fringes in Young's double slit experiment and the diffraction pattern obtained due to a narrow single slit.
In Young’s double slit experiment to produce interference pattern, obtain the conditions for constructive and destructive interference. Hence deduce the expression for the fringe width.
The slits in a Young's double slit experiment have equal width and the source is placed symmetrically with respect to the slits. The intensity at the central fringe is I0. If one of the slits is closed, the intensity at this point will be ____________ .
A thin transparent sheet is placed in front of a Young's double slit. The fringe-width will _____________ .
A Young's double slit apparatus has slits separated by 0⋅28 mm and a screen 48 cm away from the slits. The whole apparatus is immersed in water and the slits are illuminated by red light \[\left( \lambda = 700\text{ nm in vacuum} \right).\] Find the fringe-width of the pattern formed on the screen.
A parallel beam of monochromatic light is used in a Young's double slit experiment. The slits are separated by a distance d and the screen is placed parallel to the plane of the slits. Slow that if the incident beam makes an angle \[\theta = \sin^{- 1} \left( \frac{\lambda}{2d} \right)\] with the normal to the plane of the slits, there will be a dark fringe at the centre P0 of the pattern.
In a Young's double slit experiment, \[\lambda = 500\text{ nm, d = 1.0 mm and D = 1.0 m.}\] Find the minimum distance from the central maximum for which the intensity is half of the maximum intensity.
Consider the arrangement shown in the figure. By some mechanism, the separation between the slits S3 and S4 can be changed. The intensity is measured at the point P, which is at the common perpendicular bisector of S1S2 and S2S4. When \[z = \frac{D\lambda}{2d},\] the intensity measured at P is I. Find the intensity when z is equal to

(a) \[\frac{D\lambda}{d}\]
(b) \[\frac{3D\lambda}{2d}\] and
(c) \[\frac{2D\lambda}{d}\]
In Young's double slit experiment using monochromatic light of wavelength 600 nm, 5th bright fringe is at a distance of 0·48 mm from the centre of the pattern. If the screen is at a distance of 80 cm from the plane of the two slits, calculate:
(i) Distance between the two slits.
(ii) Fringe width, i.e. fringe separation.
In Young's double-slit experiment, the two slits are separated by a distance of 1.5 mm, and the screen is placed 1 m away from the plane of the slits. A beam of light consisting of two wavelengths of 650 nm and 520 nm is used to obtain interference fringes.
Find the distance of the third bright fringe for λ = 520 nm on the screen from the central maximum.
Answer the following question.
Write the conditions on path difference under which (i) constructive (ii) destructive interference occur in Young's double-slit experiment.
When a beam of light is used to determine the position of an object, the maximum accuracy is achieved, if the light is ______.
A thin circular ring of mass M and radius R is rotating about its axis with a constant angular velocity ω. Two objects each of mass m are attached gently to the opposite ends of diameter of the ring. The ring will now rotate with an angular velocity:
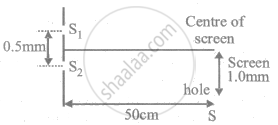
In Young's double slit experiment shown in figure S1 and S2 are coherent sources and S is the screen having a hole at a point 1.0 mm away from the central line. White light (400 to 700 nm) is sent through the slits. Which wavelength passing through the hole has strong intensity?
How will the interference pattern in Young's double-slit experiment be affected if the source slit is moved away from the plane of the slits?
In a double-slit experiment with monochromatic light, fringes are obtained on a screen placed at some distance from the plane of slits. If the screen is moved by 5 × 10-2 m towards the slits, the change in fringe width is 3 × 10-3 cm. If the distance between the slits is 1 mm, then the wavelength of the light will be ______ nm.
In a Young's double slit experiment, the width of the one of the slit is three times the other slit. The amplitude of the light coming from a slit is proportional to the slit- width. Find the ratio of the maximum to the minimum intensity in the interference pattern.
A fringe width of 6 mm was produced for two slits separated by 1 mm apart. The screen is placed 10 m away. The wavelength of light used is 'x' nm. The value of 'x' to the nearest integer is ______.
Interference fringes are observed on a screen by illuminating two thin slits 1 mm apart with a light source (λ = 632.8 nm). The distance between the screen and the slits is 100 cm. If a bright fringe is observed on a screen at distance of 1.27 mm from the central bright fringe, then the path difference between the waves, which are reaching this point from the slits is close to :
- Assertion (A): In Young's double slit experiment all fringes are of equal width.
- Reason (R): The fringe width depends upon the wavelength of light (λ) used, the distance of the screen from the plane of slits (D) and slits separation (d).
