Advertisements
Advertisements
प्रश्न
Define relaxation time of the free electrons drifting in a conductor. How is it related to the drift velocity of free electrons? Use this relation to deduce the expression for the electrical resistivity of the material.
उत्तर
Relaxation time (τ), it is the short time for which a free electron accelerates before it undergoes a collision with the positive ion in the conductor. Or, we can say it is the average time elapsed between two successive collisions. It is of the order 10−14 s. It decreases with increase of temperature and is given as
`vecV_d = vecatau`
`or vecV_d = (-eE)/m tau [because veca =-(evecE)/m]`
Where `vecV_d` is the drift velocity E is the applied electric field. e and m are the charge and mass of electron respectively.
Again consider the conductor with length l and A as area of cross-section. Let n be the number of electrons per unit volume in the conductor.
`V_d = -(eE)/m tau`(Magnitude of drift velocity)
The current flowing through the conductor due to drift
I = nAvde
Substituting value of νd
`I = nA ((eEtau)/m)e`
`I = (nAe^2Etau)/m`
If V is potential difference applied across the two ends then
`E = V/l`put in above equation
`So I = (nAe^2Vtau)/(ml)`
`V/I = (ml)/("ne"^2tauA)`
Now, According to ohm’s law `V/1 = R`(Resistance of conductor)
Thus,
`R = m/("ne"^2tau) l/A`
Compare this with formula of resistance `R =rho*l/A`
Where ρ is the resistivity of the material we get
`rho = m/("ne"^2tau)`
Thus electrical resistivity depends inversely on the relaxation time τ.
संबंधित प्रश्न
Why alloys like constantan and manganin are used for making standard resistors?
Electrons are emitted by a hot filament and are accelerated by an electric field, as shown in the figure. The two stops at the left ensure that the electron beam has a uniform cross-section.
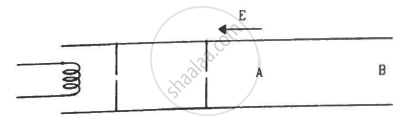
A current of 1.0 A exists in a copper wire of cross-section 1.0 mm2. Assuming one free electron per atom, calculate the drift speed of the free electrons in the wire. The density of copper is 9000 kg m–3.
Consider the following statements.
(A) Free-electron density is different in different metals.
(B) Free-electron density in a metal depends on temperature.
Thomson Effect is caused _______________ .
The position-time relation of a particle moving along the x-axis is given by x = a - bt + ct2 where a, band c are positive numbers. The velocity-time graph of the particle is ______.
The identical conductors maintained at same temperature are given potential difference in the ratio 1 : 2. Then the ratio of their drift velocities is ______.
Is the momentum conserved when charge crosses a junction in an electric circuit? Why or why not?
The potential difference applied across a given conductor is doubled. How will this affect (i) the mobility of electrons and (ii) the current density in the conductor? Justify your answers.
The drift velocity of electrons in a conductor connected to a battery is given by vd = `(−"eE" τ)/"m"`. Here, e is the charge of the electron, E is the electric field, τ is the average time between collisions and m is the mass of the electron.
Based on this, answer the following:
- How does the drift velocity change with a change in the potential difference across the conductor?
- A copper wire of length 'l' is connected to a source. If the copper wire is replaced by another copper wire of the same area of cross-section but of length '4l', how will the drift velocity change? Explain your answer.
