Advertisements
Advertisements
प्रश्न
Electrons are emitted by a hot filament and are accelerated by an electric field, as shown in the figure. The two stops at the left ensure that the electron beam has a uniform cross-section.
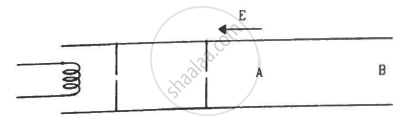
पर्याय
The speed of the electrons is more at B than at A
The electric current is from left to right
The magnitude of the current is larger at B than at A
The current density is more at B than at A
उत्तर
The speed of the electrons is more at B than at A
Let the potentials at A and B be VA and VB.
As potential,
\[E = - \frac{dV}{dr}\]
potential increases in the direction opposite to the direction of the electric field.
Thus, VA < VB
Potential energy of the electrons at points A and B:-
UA = -eVA
UB = -eVB
Thus, UA > UB
Let the kinetic energy of an electron at points A and B be KA and KB respectively.
Applying the principle of conservation of mechanical energy, we get:-
UA + KA = UB + KB
As, UA > UB,
KA < KB
Therefore, the speed of the electrons is more at B than at A.
APPEARS IN
संबंधित प्रश्न
Derive an expression for drift velocity of free electrons.
Estimate the average drift speed of conduction electrons in a copper wire of cross-sectional area 2.5 × 10−7 m2 carrying a current of 1.8 A. Assume the density of conduction electrons to be 9 × 1028 m−3.
Estimate the average drift speed of conduction electrons in a copper wire of cross-sectional area 1.0 × 10−7 m2 carrying a current of 1.5 A. Assume the density of conduction electrons to be 9 × 1028 m−3
Estimate the average drift speed of conduction electrons in a copper wire of cross-sectional area 2·5 × 10−7 m2 carrying a current of 2·7 A. Assume the density of conduction electrons to be 9 × 1028 m−3
How does drift velocity of electrons in a metallic conductor vary with increase in temperature? Explain.
(a) drift speed
(b) current density
(c) electric current
(d) electric field
Explain the term ‘drift velocity’ of electrons in conductor. Hence obtain the expression for the current through a conductor in terms of ‘drift velocity’.
Define relaxation time of the free electrons drifting in a conductor. How is it related to the drift velocity of free electrons? Use this relation to deduce the expression for the electrical resistivity of the material.
Derive an expression for drift velocity of free electrons in a conductor in terms of relaxation time.
Consider a wire of length 4 m and cross-sectional area 1 mm2 carrying a current of 2 A. If each cubic metre of the material contains 1029 free electrons, find the average time taken by an electron to cross the length of the wire.
Consider the following statements.
(A) Free-electron density is different in different metals.
(B) Free-electron density in a metal depends on temperature.
Peltier Effect is caused _______________ .
Obtain the expression for the current flowing through a conductor having number density of the electron n, area of cross-section A in terms of the drift velocity vd .
When a current I is set up in a wire of radius r, the drift velocity is vd· If the same current is set up through a wire of radius 2 r, the drift velocity will be:
The relaxation time τ is nearly independent of applied E field whereas it changes significantly with temperature T. First fact is (in part) responsible for Ohm’s law whereas the second fact leads to variation of ρ with temperature. Elaborate why?
Consider two conducting wires A and B of the same diameter but made of different materials joined in series across a battery. The number density of electrons in A is 1.5 times that in B. Find the ratio of the drift velocity of electrons in wire A to that in wire B.
The drift velocity of electrons in a conductor connected to a battery is given by vd = `(−"eE" τ)/"m"`. Here, e is the charge of the electron, E is the electric field, τ is the average time between collisions and m is the mass of the electron.
Based on this, answer the following:
- How does the drift velocity change with a change in the potential difference across the conductor?
- A copper wire of length 'l' is connected to a source. If the copper wire is replaced by another copper wire of the same area of cross-section but of length '4l', how will the drift velocity change? Explain your answer.
