Advertisements
Advertisements
प्रश्न
Explain the term ‘drift velocity’ of electrons in conductor. Hence obtain the expression for the current through a conductor in terms of ‘drift velocity’.
उत्तर
‘Drift velocity’ of electrons in a conductor - Metals contain a large number of free electrons. These electrons are in continuous random motion. Due to the random motion, the free electrons collide with positive metal ions with high frequency and undergo change in direction at each collision. So the average velocity for the electrons in a conductor is zero.
Now, when this conductor is connected to a source of emf, an electric field is established in the conductor, such that E = `"V"/"L"`
Where V= potential difference across the conductor and
L = length of the conductor.
The electric field exerts an electrostatic force ‘-Ee’ on each free electron in the conductor. The acceleration of each electron is given by
`vec"a" = ("e"vec"E")/"m"`
Where e = electric charge on electron and
m = mass of electron
The negative sign indicates that the force and hence the acceleration is in a direction opposite to the direction of the electric field. Due to this acceleration, the electrons attain a velocity in addition to thermal velocity in the direction opposite to that of electric field.
The average velocity of all the free electrons in the conductor is called the drift velocity of free electrons of the conductor.
`vec"v"_"d" = - ("e"vec"E")/"m" tau` ....... (1)
Thus, the expression for the drift velocity is
Electric field, `"E" = - "V"/"L"` .....(2)
where `tau` = relaxation time between two successive collision.
Let n = number density of electrons in the conductor.
No. of free electrons in the conductor = nAL
Total charge on the conductor, q = nALe
Time taken by this charge to cover the length L of the conductor, `"t" = "L"/"V"_"d"`
current `"I" = "q"/"t"`
`= ("nALe")/"L" xx "v"_"d"`
`= "nAev"_"d"`
Using eq (1) and (2) , we get that
`"I" = "nAe" xx (-("e"vec"E")/"m" tau)`
`= "nAe" xx (- ("e"(-"V"))/("mL") tau)`
`= (("n" "e"^"2A")/("mL")tau)"V"`
APPEARS IN
संबंधित प्रश्न
Derive an expression for drift velocity of free electrons.
The number density of free electrons in a copper conductor is 8.5 × 1028 m−3. How long does an electron take to drift from one end of a wire 3.0 m long to its other end? The area of cross-section of the wire is 2.0 × 10−6 m2 and it is carrying a current of 3.0 A.
How does drift velocity of electrons in a metallic conductor vary with increase in temperature? Explain.
Electrons are emitted by a hot filament and are accelerated by an electric field, as shown in the figure. The two stops at the left ensure that the electron beam has a uniform cross-section.
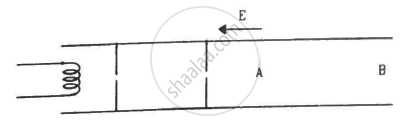
Consider the following statements.
(A) Free-electron density is different in different metals.
(B) Free-electron density in a metal depends on temperature.
Thomson Effect is caused _______________ .
Obtain the expression for the current flowing through a conductor having number density of the electron n, area of cross-section A in terms of the drift velocity vd .
Define relaxation time.
Consider two conducting wires A and B of the same diameter but made of different materials joined in series across a battery. The number density of electrons in A is 1.5 times that in B. Find the ratio of the drift velocity of electrons in wire A to that in wire B.
A potential difference (V) is applied across a conductor of length 'L' and cross-sectional area 'A'.
How will the drift velocity of electrons and the current density be affected if another identical conductor of the same material were connected in series with the first conductor? Justify your answers.
