Advertisements
Advertisements
प्रश्न
Define relaxation time.
उत्तर
Relaxation time is the time interval between two successive collisions of electrons in a conductor when current flows.
संबंधित प्रश्न
Why alloys like constantan and manganin are used for making standard resistors?
When electrons drift in a metal from lower to higher potential, does it mean that all the free electrons of the metal are moving in the same direction?
Define relaxation time of the free electrons drifting in a conductor. How is it related to the drift velocity of free electrons? Use this relation to deduce the expression for the electrical resistivity of the material.
A conductor of length ‘l’ is connected to a dc source of potential ‘V’. If the length of the conductor is tripled by gradually stretching it, keeping ‘V’ constant, how will (i) drift speed of electrons and (ii) resistance of the conductor be affected? Justify your answer.
When a current is established in a wire, the free electrons drift in the direction opposite to the current. Does the number of free electrons in the wire continuously decrease?
Electrons are emitted by a hot filament and are accelerated by an electric field, as shown in the figure. The two stops at the left ensure that the electron beam has a uniform cross-section.
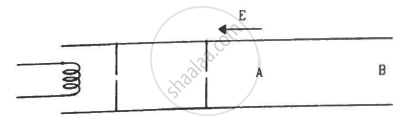
A current of 1.0 A exists in a copper wire of cross-section 1.0 mm2. Assuming one free electron per atom, calculate the drift speed of the free electrons in the wire. The density of copper is 9000 kg m–3.
The potential difference applied across a given conductor is doubled. How will this affect (i) the mobility of electrons and (ii) the current density in the conductor? Justify your answers.
A potential difference (V) is applied across a conductor of length 'L' and cross-sectional area 'A'.
How will the drift velocity of electrons and the current density be affected if another identical conductor of the same material were connected in series with the first conductor? Justify your answers.
The drift velocity of electrons in a conductor connected to a battery is given by vd = `(−"eE" τ)/"m"`. Here, e is the charge of the electron, E is the electric field, τ is the average time between collisions and m is the mass of the electron.
Based on this, answer the following:
- How does the drift velocity change with a change in the potential difference across the conductor?
- A copper wire of length 'l' is connected to a source. If the copper wire is replaced by another copper wire of the same area of cross-section but of length '4l', how will the drift velocity change? Explain your answer.
