Advertisements
Advertisements
प्रश्न
A parallel plate capacitor (A) of capacitance C is charged by a battery to voltage V. The battery is disconnected and an uncharged capacitor (B) of capacitance 2C is connected across A. Find the ratio of total electrostatic energy stored in A and B finally and that stored in A initially.
उत्तर
The electric field in the region between the plates depends on the change given to the conducting plates,
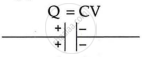
For capacitor 'A' of capacitance C, having voltage V, the charge on it is given by Q = CV.
On connecting this capacitor A with capacitor B changes get distributed.
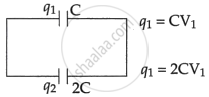
The total electrostatic energy stored in A is given by
`U_A = 1/2CV^2 = 1/2 Q^2/C` .........(i)
Since capacitor B is connected across capacitor A.
∴ `C_"net" = C_A + C_B`
= C + 2C
= 3C
∴ Total electrostatic energy in A and B is given by
`U_"net" = 1/2 Q^2/C_"net"`
= `1/2(Q^2/(3C))` ....(since total change Q remains constant)
= `1/3(1/2 Q^2/C)`
= `1/3U_A` .....[By equation (i)]
`U_"net"/U_A = 1/3`
APPEARS IN
संबंधित प्रश्न
A 100 μF capacitor is joined to a 24 V battery through a 1.0 MΩ resistor. Plot qualitative graphs (a) between current and time for the first 10 minutes and (b) between charge and time for the same period.
Two capacitors of capacitances 4⋅0 µF and 6⋅0 µF are connected in series with a battery of 20 V. Find the energy supplied by the battery.
A capacitance C charged to a potential difference V is discharged by connecting its plates through a resistance R. Find the heat dissipated in one time constant after the connections are made. Do this by calculating ∫ i2R dt and also by finding the decrease in the energy stored in the capacitor.
Find the charge on each of the capacitors 0.20 ms after the switch S is closed in the figure.
A capacitor with stored energy 4⋅0 J is connected with an identical capacitor with no electric field in between. Find the total energy stored in the two capacitors.
A capacitor of capacitance C is given a charge Q. At t = 0, it is connected to an uncharged capacitor of equal capacitance through a resistance R. Find the charge on the second capacitor as a function of time.
A metal sphere of radius R is charged to a potential V.
- Find the electrostatic energy stored in the electric field within a concentric sphere of radius 2 R.
- Show that the electrostatic field energy stored outside the sphere of radius 2 R equals that stored within it.
Answer the following question.
Obtain the expression for the energy stored in a capacitor connected across a dc battery. Hence define energy density of the capacitor
A capacitor is a device that stores ____________.
A parallel plate condenser is immersed in an oil of dielectric constant 2. The field between the plates is ______.
