Advertisements
Advertisements
प्रश्न
Answer the following question.
Obtain the expression for the energy stored in a capacitor connected across a dc battery. Hence define energy density of the capacitor
उत्तर
Energy Stored in a Charged Capacitor:
The energy of a charged capacitor is measured by the total work done in charging the capacitor to a given potential.
Let us assume that initially both the plates are uncharged. Now, we have to repeatedly remove small positive charges from one plate and transfer them to the other plate.
Let
q →Total quantity of charge transferred
V →Potential difference between the two plates
Then,
q = CV
Now, when an additional small charge dq is transferred from the negative plate to the positive plate, the small work done is given by,
`dW = Vdq = q/"C" dq`
The total work done in transferring charge Q is given by,
`W = int_0^Q q/"C"dq = 1/"C"int_0^Qqdq = 1/"C"[q^2/2]_0^Q`
`W = Q^2/(2"C")`
This work done is stored as electrostatic potential energy U in the capacitor.
`U = Q^2/(2"C")`
Hence energy stored in the capacitor = `1/2 Q^2/"C" = (Asigma)^2/2 xx d/(epsilon_oA)`
The surface charge density `sigma` is related to the electric field `E` between the plates, `E` = `sigma/epsilon_o`
So, energy stored in the capacitor = `1/2epsilon_oE^2 xx Ad`
Here, Ad is volume between the plates of capacitor.
We define energy density as energy stored per unit volume of space.
Energy density of electric field = `U = 1/2epsilon_oE^2`
APPEARS IN
संबंधित प्रश्न
A 12 pF capacitor is connected to a 50 V battery. How much electrostatic energy is stored in the capacitor?
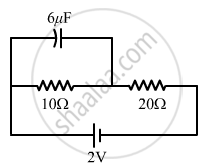
Find the charge on the capacitor as shown in the circuit.
A capacitor of capacitance 500 μF is connected to a battery through a 10 kΩ resistor. The charge stored in the capacitor in the first 5 s is larger than the charge stored in the next.
(a) 5 s
(b) 50 s
(c) 500 s
(d) 500 s
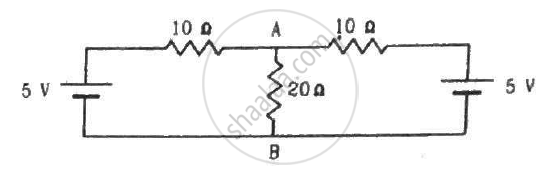
(a) Find the current in the 20 Ω resistor shown in the figure. (b) If a capacitor of capacitance 4 μF is joined between the points A and B, what would be the electrostatic energy stored in it in steady state?
Two capacitors of capacitances 4⋅0 µF and 6⋅0 µF are connected in series with a battery of 20 V. Find the energy supplied by the battery.
A capacitance C charged to a potential difference V is discharged by connecting its plates through a resistance R. Find the heat dissipated in one time constant after the connections are made. Do this by calculating ∫ i2R dt and also by finding the decrease in the energy stored in the capacitor.
By evaluating ∫i2Rdt, show that when a capacitor is charged by connecting it to a battery through a resistor, the energy dissipated as heat equals the energy stored in the capacitor.
A capacitor with stored energy 4⋅0 J is connected with an identical capacitor with no electric field in between. Find the total energy stored in the two capacitors.
A capacitor of capacitance C is given a charge Q. At t = 0, it is connected to an uncharged capacitor of equal capacitance through a resistance R. Find the charge on the second capacitor as a function of time.
A capacitor of capacitance C is given a charge Q. At t = 0, it is connected to an ideal battery of emf ε through a resistance R. Find the charge on the capacitor at time t.
