Advertisements
Advertisements
प्रश्न
Two capacitors of capacitances 4⋅0 µF and 6⋅0 µF are connected in series with a battery of 20 V. Find the energy supplied by the battery.
उत्तर
Given :
`C_1 = 4 "uF"`
`C_2 = 6 "uF"`
`V = 20 V`
Now,
The equivalent capacitance is given by
`C_(eq) =( C_1C_2)/(C_1+C_2) = (4 xx 6)/(4+6) = 2.4 "uF"`
The energy supplied by the battery is given by
`E = C_(eq) V^2`
= `(2.4 "uF") xx (20)^2`
= `(2.4 "uF") xx 400 = 960 "uJ"`
APPEARS IN
संबंधित प्रश्न
A 12 pF capacitor is connected to a 50 V battery. How much electrostatic energy is stored in the capacitor?
A 600 pF capacitor is charged by a 200 V supply. It is then disconnected from the supply and is connected to another uncharged 600 pF capacitor. How much electrostatic energy is lost in the process?
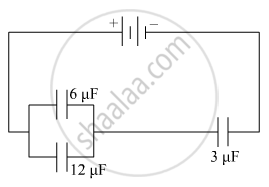
In the following arrangement of capacitors, the energy stored in the 6 µF capacitor is E. Find the value of the following :
(i) Energy stored in 12 µF capacitor.
(ii) Energy stored in 3 µF capacitor.
(iii) Total energy drawn from the battery.
A capacitor of capacitance 500 μF is connected to a battery through a 10 kΩ resistor. The charge stored in the capacitor in the first 5 s is larger than the charge stored in the next.
(a) 5 s
(b) 50 s
(c) 500 s
(d) 500 s
A capacitor C1 of capacitance 1 μF and a capacitor C2 of capacitance 2 μF are separately charged by a common battery for a long time. The two capacitors are then separately discharged through equal resistors. Both the discharge circuits are connected at t = 0.
(a) The current in each of the two discharging circuits is zero at t = 0.
(b) The currents in the two discharging circuits at t = 0 are equal but not zero.
(c) The currents in the two discharging circuits at t = 0 are unequal.
(d) C1 loses 50% of its initial charge sooner than C2 loses 50% of its initial charge.
A 20 μF capacitor is joined to a battery of emf 6.0 V through a resistance of 100 Ω. Find the charge on the capacitor 2.0 ms after the connections are made.
A 100 μF capacitor is joined to a 24 V battery through a 1.0 MΩ resistor. Plot qualitative graphs (a) between current and time for the first 10 minutes and (b) between charge and time for the same period.
How many time constants will elapse before the energy stored in the capacitor reaches half of its equilibrium value in a charging RC circuit?
A capacitor of capacitance 12.0 μF is connected to a battery of emf 6.00 V and internal resistance 1.00 Ω through resistanceless leads. 12.0 μs after the connections are made, what will be (a) the current in the circuit (b) the power delivered by the battery (c) the power dissipated in heat and (d) the rate at which the energy stored in the capacitor is increasing?
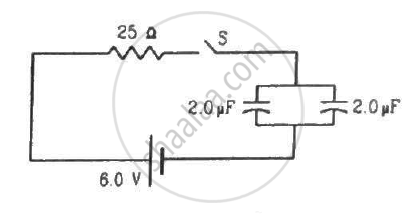
Find the charge on each of the capacitors 0.20 ms after the switch S is closed in the figure.
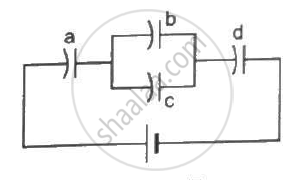
Each capacitor in figure has a capacitance of 10 µF. The emf of the battery is 100 V. Find the energy stored in each of the four capacitors.
A point charge Q is placed at the origin. Find the electrostatic energy stored outside the sphere of radius R centred at the origin.
Answer the following question.
Obtain the expression for the energy stored in a capacitor connected across a dc battery. Hence define energy density of the capacitor
A capacitor is a device that stores ____________.
A 2µF capacitor is charge to 100 volt and then its plate are connected by a conducting wire. The heat produced is:-
A parallel plate capacitor has a uniform electric field `overset(->)("E")` in the space between the plates. If the distance between the plates is ‘d’ and the area of each plate is ‘A’, the energy stored in the capacitor is ______
(ε0 = permittivity of free space)
Electrostatic energy of 4 x 10−4 J is stored in a charged 25 pF capacitor. Find the charge on the capacitor.
In a capacitor of capacitance 20 µF, the distance between the plates is 2 mm. If a dielectric slab of width 1 mm and dielectric constant 2 is inserted between the plates, what is the new capacitance?
