Advertisements
Advertisements
प्रश्न
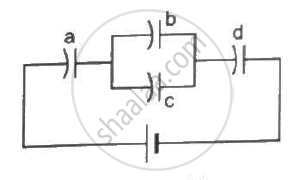
Each capacitor in figure has a capacitance of 10 µF. The emf of the battery is 100 V. Find the energy stored in each of the four capacitors.
उत्तर
Capacitors b and c are in parallel; their equivalent capacitance is 20 µF.
Thus, the net capacitance of the circuit is given by
`1/C_"net" = 1/10 + 1/20 + 1/10`
`⇒ 1/C_"net" = (2+1+2)/20 = 5/20`
`⇒ C_"net" = 4 "uF"`
The total charge of the battery is given by
`Q = C_"net"V = (4 "uF") xx (100 "V") = 4 xx 10^-4 C`
For a and d,
`q = 4 xx 10^-4 "C" and "C" = 10^-5 "F"`
`therefore E = q^2/(2C) = (4 xx 10^-4)/(2 xx 10^-5)`
`⇒ E = 8 xx 10^-3 "J" = 8 "mJ"`
For b and c,
`q = 4 xx 10^-4 "C" and "C"_(eq) = 2"C" = 2 xx 10^-5 "F"`
`therefore V = q/C_(eq) (4 xx 10^-4)/(2 xx 10^-5) = 20 V`
`⇒ E = 1/2 CV^2`
`⇒ E = 1/2 xx 10^-5 xx 400`
`⇒ E = 2 xx 10^-3 "J" = 2 "mJ"`
APPEARS IN
संबंधित प्रश्न
Explain what would happen if the capacitor given in previous question a 3 mm thick mica sheet (of dielectric constant = 6) were inserted between the plates,
- While the voltage supply remained connected.
- After the supply was disconnected.
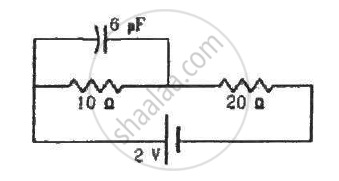
Find the charge on the capacitor shown in the figure.
A 20 μF capacitor is joined to a battery of emf 6.0 V through a resistance of 100 Ω. Find the charge on the capacitor 2.0 ms after the connections are made.
The plates of a capacitor of capacitance 10 μF, charged to 60 μC, are joined together by a wire of resistance 10 Ω at t = 0. Find the charge on the capacitor in the circuit at (a) t = 0 (b) t = 30 μs (c) t = 120 μs and (d) t = 1.0 ms.
How many time constants will elapse before the current in a charging RC circuit drops to half of its initial value? Answer the same question for a discharging RC circuit.
How many time constants will elapse before the energy stored in the capacitor reaches half of its equilibrium value in a charging RC circuit?
A capacitor of capacitance C is connected to a battery of emf ε at t = 0 through a resistance R. Find the maximum rate at which energy is stored in the capacitor. When does the rate have this maximum value?
A large conducting plane has a surface charge density `1.0 xx 10^-4 "Cm"^-2` . Find the electrostatic energy stored in a cubical volume of edge 1⋅0 cm in front of the plane.
Answer the following question.
Obtain the expression for the energy stored in a capacitor connected across a dc battery. Hence define energy density of the capacitor
A capacitor is a device that stores ____________.
If the p. d. across a capacitor is increased from 10 V to 30 V, then the energy stored with the capacitor ____________.
A parallel plate condenser is immersed in an oil of dielectric constant 2. The field between the plates is ______.
A capacitor is charged by a battery and energy stored is 'U'. Now the battery is removed and the distance between plates is increased to four times. The energy stored becomes ______.
An air-filled parallel plate capacitor has a uniform electric field `overset(->)("E")` in the space between the plates. If the distance between the plates is 'd' and the area of each plate is 'A', the energy stored in the capacitor is ______
(∈0 = permittivity of free space)
What fraction of the energy drawn from the charging battery is stored in a capacitor?
Prove that, if an insulated, uncharged conductor is placed near a charged conductor and no other conductors are present, the uncharged body must be intermediate in potential between that of the charged body and that of infinity.
A parallel plate capacitor (A) of capacitance C is charged by a battery to voltage V. The battery is disconnected and an uncharged capacitor (B) of capacitance 2C is connected across A. Find the ratio of total electrostatic energy stored in A and B finally and that stored in A initially.
Derive an expression for energy stored in a capacitor.
In a capacitor of capacitance 20 µF, the distance between the plates is 2 mm. If a dielectric slab of width 1 mm and dielectric constant 2 is inserted between the plates, what is the new capacitance?
