Advertisements
Advertisements
प्रश्न
Derive an expression for energy stored in a capacitor.
Derive an expression for energy stored in a charged capacitor.
उत्तर
Consider a capacitor of capacitance C being charged by a DC source of V volt as shown in figure.

Capacitor charged by a DC source.
During the process of charging, let q' be the charge on the capacitor and V be the potential difference between the plates. Hence
`"C" =("q""'")/"V"`
A small amount of work is done if a small charge dq is further transferred between the plates.
∴ `"dW" ="Vdq"=("q""'")/"Cdq"`
Total work done in transferring the charge
`"W"=int"dw"=int_0^"Q" ("q'")/"C" "dq" = 1/"C"int_0^"Q" "q'" "dq"`
`=1/"C"[(("q""'")^2)/2]_0^"Q" = 1/2 "Q"^2/"C"`
This work done is stored as electrical potential energy U of the capacitor. This work done can be expressed in different forms as follows:
∴ `"U" = 1/2 "Q"^2/"C"=1/2"CV"^2=1/2"QV" (because "Q" = "CV")`
Notes
Students should refer to the answer according to their questions.
APPEARS IN
संबंधित प्रश्न
A 12 pF capacitor is connected to a 50 V battery. How much electrostatic energy is stored in the capacitor?
A 600 pF capacitor is charged by a 200 V supply. It is then disconnected from the supply and is connected to another uncharged 600 pF capacitor. How much electrostatic energy is lost in the process?
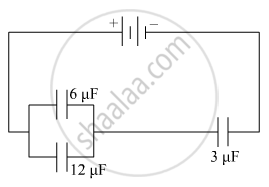
In the following arrangement of capacitors, the energy stored in the 6 µF capacitor is E. Find the value of the following :
(i) Energy stored in 12 µF capacitor.
(ii) Energy stored in 3 µF capacitor.
(iii) Total energy drawn from the battery.
A capacitor of capacitance 500 μF is connected to a battery through a 10 kΩ resistor. The charge stored in the capacitor in the first 5 s is larger than the charge stored in the next.
(a) 5 s
(b) 50 s
(c) 500 s
(d) 500 s
A capacitance C, a resistance R and an emf ε are connected in series at t = 0. What is the maximum value of (a) the potential difference across the resistor (b) the current in the circuit (c) the potential difference across the capacitor (d) the energy stored in the capacitor (e) the power delivered by the battery and (f) the power converted into heat?
A 20 μF capacitor is joined to a battery of emf 6.0 V through a resistance of 100 Ω. Find the charge on the capacitor 2.0 ms after the connections are made.
The plates of a capacitor of capacitance 10 μF, charged to 60 μC, are joined together by a wire of resistance 10 Ω at t = 0. Find the charge on the capacitor in the circuit at (a) t = 0 (b) t = 30 μs (c) t = 120 μs and (d) t = 1.0 ms.
How many time constants will elapse before the current in a charging RC circuit drops to half of its initial value? Answer the same question for a discharging RC circuit.
How many time constants will elapse before the charge on a capacitors falls to 0.1% of its maximum value in a discharging RC circuit?
By evaluating ∫i2Rdt, show that when a capacitor is charged by connecting it to a battery through a resistor, the energy dissipated as heat equals the energy stored in the capacitor.
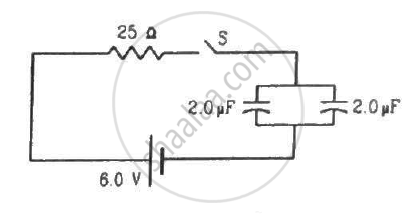
Find the charge on each of the capacitors 0.20 ms after the switch S is closed in the figure.
A capacitor with stored energy 4⋅0 J is connected with an identical capacitor with no electric field in between. Find the total energy stored in the two capacitors.
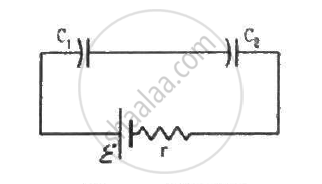
Consider the situation shown in figure. The switch is closed at t = 0 when the capacitors are uncharged. Find the charge on the capacitor C1 as a function of time t.
A capacitor of capacitance C is given a charge Q. At t = 0, it is connected to an ideal battery of emf ε through a resistance R. Find the charge on the capacitor at time t.
A point charge Q is placed at the origin. Find the electrostatic energy stored outside the sphere of radius R centred at the origin.
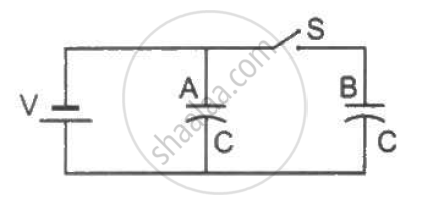
Figure shows two identical parallel plate capacitors connected to a battery through a switch S. Initially, the switch is closed so that the capacitors are completely charged. The switch is now opened and the free space between the plates of the capacitors is filled with a dielectric of dielectric constant 3. Find the ratio of the initial total energy stored in the capacitors to the final total energy stored.
A capacitor is a device that stores ____________.
If the p. d. across a capacitor is increased from 10 V to 30 V, then the energy stored with the capacitor ____________.
A parallel plate condenser is immersed in an oil of dielectric constant 2. The field between the plates is ______.
A capacitor is charged by a battery and energy stored is 'U'. Now the battery is removed and the distance between plates is increased to four times. The energy stored becomes ______.
What fraction of the energy drawn from the charging battery is stored in a capacitor?
A parallel plate capacitor has a uniform electric field `overset(->)("E")` in the space between the plates. If the distance between the plates is ‘d’ and the area of each plate is ‘A’, the energy stored in the capacitor is ______
(ε0 = permittivity of free space)
Prove that, if an insulated, uncharged conductor is placed near a charged conductor and no other conductors are present, the uncharged body must be intermediate in potential between that of the charged body and that of infinity.
A fully charged capacitor C with initial charge q0 is connected to a coil of self-inductance L at t = 0. The time at which the energy is stored equally between the electric and magnetic fields is ______.
In a capacitor of capacitance 20 µF, the distance between the plates is 2 mm. If a dielectric slab of width 1 mm and dielectric constant 2 is inserted between the plates, what is the new capacitance?
