Advertisements
Advertisements
प्रश्न
How many time constants will elapse before the charge on a capacitors falls to 0.1% of its maximum value in a discharging RC circuit?
उत्तर
The decay of charge across a capacitor,
\[q = Q e^{- \frac{t}{RC}}\]
Here, q = 0.1 % and Q = 1 × 10−3 Q
⇒ 1 × 10−3 Q = \[Q e^{- \frac{t}{RC}}\]
\[\Rightarrow e^{- \frac{t}{RC}}=10^{-3}\]
\[\Rightarrow \frac{t}{rC} = - \left( - 6 . 9 \right) = 6 . 9\]
Let t = nRC
\[\Rightarrow \frac{nRC}{RC} = 6 . 9\]
\[ \Rightarrow n = 6 . 9\]
APPEARS IN
संबंधित प्रश्न
A 600 pF capacitor is charged by a 200 V supply. It is then disconnected from the supply and is connected to another uncharged 600 pF capacitor. How much electrostatic energy is lost in the process?
Find the ratio of energy stored in the two configurations if they are both connected to the same source.
The energy density in the electric field created by a point charge falls off with the distance from the point charge as
The plates of a capacitor of capacitance 10 μF, charged to 60 μC, are joined together by a wire of resistance 10 Ω at t = 0. Find the charge on the capacitor in the circuit at (a) t = 0 (b) t = 30 μs (c) t = 120 μs and (d) t = 1.0 ms.
How many time constants will elapse before the current in a charging RC circuit drops to half of its initial value? Answer the same question for a discharging RC circuit.
A capacitor of capacitance C is connected to a battery of emf ε at t = 0 through a resistance R. Find the maximum rate at which energy is stored in the capacitor. When does the rate have this maximum value?
A capacitance C charged to a potential difference V is discharged by connecting its plates through a resistance R. Find the heat dissipated in one time constant after the connections are made. Do this by calculating ∫ i2R dt and also by finding the decrease in the energy stored in the capacitor.
By evaluating ∫i2Rdt, show that when a capacitor is charged by connecting it to a battery through a resistor, the energy dissipated as heat equals the energy stored in the capacitor.
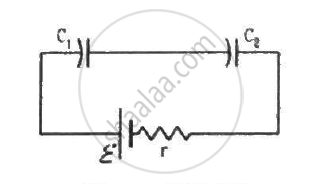
Consider the situation shown in figure. The switch is closed at t = 0 when the capacitors are uncharged. Find the charge on the capacitor C1 as a function of time t.
A capacitor of capacitance C is given a charge Q. At t = 0, it is connected to an ideal battery of emf ε through a resistance R. Find the charge on the capacitor at time t.
A point charge Q is placed at the origin. Find the electrostatic energy stored outside the sphere of radius R centred at the origin.
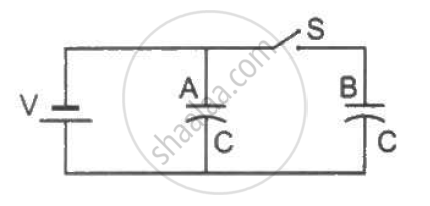
Figure shows two identical parallel plate capacitors connected to a battery through a switch S. Initially, the switch is closed so that the capacitors are completely charged. The switch is now opened and the free space between the plates of the capacitors is filled with a dielectric of dielectric constant 3. Find the ratio of the initial total energy stored in the capacitors to the final total energy stored.
If the p. d. across a capacitor is increased from 10 V to 30 V, then the energy stored with the capacitor ____________.
Do free electrons travel to region of higher potential or lower potential?
Prove that, if an insulated, uncharged conductor is placed near a charged conductor and no other conductors are present, the uncharged body must be intermediate in potential between that of the charged body and that of infinity.
A fully charged capacitor C with initial charge q0 is connected to a coil of self-inductance L at t = 0. The time at which the energy is stored equally between the electric and magnetic fields is ______.
Electrostatic energy of 4 x 10−4 J is stored in a charged 25 pF capacitor. Find the charge on the capacitor.
In a capacitor of capacitance 20 µF, the distance between the plates is 2 mm. If a dielectric slab of width 1 mm and dielectric constant 2 is inserted between the plates, what is the new capacitance?
