Advertisements
Advertisements
Question
A parallel plate capacitor (A) of capacitance C is charged by a battery to voltage V. The battery is disconnected and an uncharged capacitor (B) of capacitance 2C is connected across A. Find the ratio of total electrostatic energy stored in A and B finally and that stored in A initially.
Solution
The electric field in the region between the plates depends on the change given to the conducting plates,
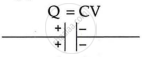
For capacitor 'A' of capacitance C, having voltage V, the charge on it is given by Q = CV.
On connecting this capacitor A with capacitor B changes get distributed.
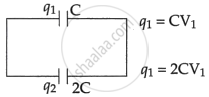
The total electrostatic energy stored in A is given by
`U_A = 1/2CV^2 = 1/2 Q^2/C` .........(i)
Since capacitor B is connected across capacitor A.
∴ `C_"net" = C_A + C_B`
= C + 2C
= 3C
∴ Total electrostatic energy in A and B is given by
`U_"net" = 1/2 Q^2/C_"net"`
= `1/2(Q^2/(3C))` ....(since total change Q remains constant)
= `1/3(1/2 Q^2/C)`
= `1/3U_A` .....[By equation (i)]
`U_"net"/U_A = 1/3`
APPEARS IN
RELATED QUESTIONS
A 600 pF capacitor is charged by a 200 V supply. It is then disconnected from the supply and is connected to another uncharged 600 pF capacitor. How much electrostatic energy is lost in the process?
A capacitor of capacitance 500 μF is connected to a battery through a 10 kΩ resistor. The charge stored in the capacitor in the first 5 s is larger than the charge stored in the next.
(a) 5 s
(b) 50 s
(c) 500 s
(d) 500 s
A capacitor C1 of capacitance 1 μF and a capacitor C2 of capacitance 2 μF are separately charged by a common battery for a long time. The two capacitors are then separately discharged through equal resistors. Both the discharge circuits are connected at t = 0.
(a) The current in each of the two discharging circuits is zero at t = 0.
(b) The currents in the two discharging circuits at t = 0 are equal but not zero.
(c) The currents in the two discharging circuits at t = 0 are unequal.
(d) C1 loses 50% of its initial charge sooner than C2 loses 50% of its initial charge.
A capacitance C, a resistance R and an emf ε are connected in series at t = 0. What is the maximum value of (a) the potential difference across the resistor (b) the current in the circuit (c) the potential difference across the capacitor (d) the energy stored in the capacitor (e) the power delivered by the battery and (f) the power converted into heat?
How many time constants will elapse before the charge on a capacitors falls to 0.1% of its maximum value in a discharging RC circuit?
By evaluating ∫i2Rdt, show that when a capacitor is charged by connecting it to a battery through a resistor, the energy dissipated as heat equals the energy stored in the capacitor.
A point charge Q is placed at the origin. Find the electrostatic energy stored outside the sphere of radius R centred at the origin.
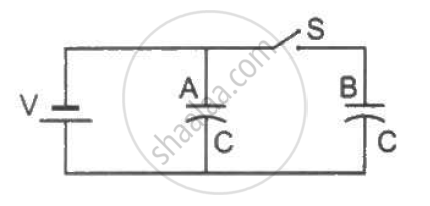
Figure shows two identical parallel plate capacitors connected to a battery through a switch S. Initially, the switch is closed so that the capacitors are completely charged. The switch is now opened and the free space between the plates of the capacitors is filled with a dielectric of dielectric constant 3. Find the ratio of the initial total energy stored in the capacitors to the final total energy stored.
Choose the correct option:
Energy stored in a capacitor and dissipated during charging a capacitor bear a ratio.
A parallel plate condenser is immersed in an oil of dielectric constant 2. The field between the plates is ______.
