Advertisements
Advertisements
प्रश्न
Consider the following statements.
(A) Free-electron density is different in different metals.
(B) Free-electron density in a metal depends on temperature.
Thomson Effect is caused _______________ .
पर्याय
due to both A and B
due to A but not due to B
due to B but not due to A
neither due to A nor due to B
उत्तर
due to B but not due to A
If a metallic conductor has non-uniform temperature distribution along its length, the density of the free electrons is different for different sections. The electrons diffuse from the sections with higher concentration to those with lower concentration of free electrons. Thus, there is an emf inside the metal that is known as Thomson emf. If a current is forced through the given conductor, positive and negative work is done on the charge carriers, depending on the direction of current. Thus, thermal energy is either produced or absorbed. Thus, the correct cause of the given effect is given by statement B alone.
APPEARS IN
संबंधित प्रश्न
Estimate the average drift speed of conduction electrons in a copper wire of cross-sectional area 2.5 × 10−7 m2 carrying a current of 1.8 A. Assume the density of conduction electrons to be 9 × 1028 m−3.
Estimate the average drift speed of conduction electrons in a copper wire of cross-sectional area 1.0 × 10−7 m2 carrying a current of 1.5 A. Assume the density of conduction electrons to be 9 × 1028 m−3
How does drift velocity of electrons in a metallic conductor vary with increase in temperature? Explain.
(a) drift speed
(b) current density
(c) electric current
(d) electric field
On the basis of electron drift, derive an expression for resistivity of a conductor in terms of number density of free electrons and relaxation time. On what factors does resistivity of a conductor depend?
Explain the term ‘drift velocity’ of electrons in conductor. Hence obtain the expression for the current through a conductor in terms of ‘drift velocity’.
Derive an expression for drift velocity of free electrons in a conductor in terms of relaxation time.
The position-time relation of a particle moving along the x-axis is given by x = a - bt + ct2 where a, band c are positive numbers. The velocity-time graph of the particle is ______.
When a current I is set up in a wire of radius r, the drift velocity is vd· If the same current is set up through a wire of radius 2 r, the drift velocity will be:
Metals are good conductor of heat than insulator because
The drift velocity of a free electron inside a conductor is ______
The identical conductors maintained at same temperature are given potential difference in the ratio 1 : 2. Then the ratio of their drift velocities is ______.
The relaxation time τ is nearly independent of applied E field whereas it changes significantly with temperature T. First fact is (in part) responsible for Ohm’s law whereas the second fact leads to variation of ρ with temperature. Elaborate why?
- Consider circuit in figure. How much energy is absorbed by electrons from the initial state of no current (ignore thermal motion) to the state of drift velocity?
- Electrons give up energy at the rate of RI2 per second to the thermal energy. What time scale would one associate with energy in problem (a)? n = no of electron/volume = 1029/m3, length of circuit = 10 cm, cross-section = A = (1mm)2
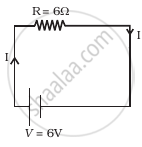
The potential difference applied across a given conductor is doubled. How will this affect (i) the mobility of electrons and (ii) the current density in the conductor? Justify your answers.
Explain how free electrons in a metal at constant temperature attain an average velocity under the action of an electric field. Hence, obtain an expression for it.
Consider two conducting wires A and B of the same diameter but made of different materials joined in series across a battery. The number density of electrons in A is 1.5 times that in B. Find the ratio of the drift velocity of electrons in wire A to that in wire B.
Two conductors, made of the same material have equal lengths but different cross-sectional areas A1 and A2 (A1 > A2). They are connected in parallel across a cell. Show that the drift velocities of electrons in two conductors are equal.
