Advertisements
Advertisements
प्रश्न
Consider the following statements.
(A) Free-electron density is different in different metals.
(B) Free-electron density in a metal depends on temperature.
Thomson Effect is caused _______________ .
विकल्प
due to both A and B
due to A but not due to B
due to B but not due to A
neither due to A nor due to B
उत्तर
due to B but not due to A
If a metallic conductor has non-uniform temperature distribution along its length, the density of the free electrons is different for different sections. The electrons diffuse from the sections with higher concentration to those with lower concentration of free electrons. Thus, there is an emf inside the metal that is known as Thomson emf. If a current is forced through the given conductor, positive and negative work is done on the charge carriers, depending on the direction of current. Thus, thermal energy is either produced or absorbed. Thus, the correct cause of the given effect is given by statement B alone.
APPEARS IN
संबंधित प्रश्न
Define the term drift velocity.
Write its (‘mobility’ of charge carriers) S.I. unit
Estimate the average drift speed of conduction electrons in a copper wire of cross-sectional area 2.5 × 10−7 m2 carrying a current of 1.8 A. Assume the density of conduction electrons to be 9 × 1028 m−3.
Estimate the average drift speed of conduction electrons in a copper wire of cross-sectional area 2·5 × 10−7 m2 carrying a current of 2·7 A. Assume the density of conduction electrons to be 9 × 1028 m−3
The number density of free electrons in a copper conductor is 8.5 × 1028 m−3. How long does an electron take to drift from one end of a wire 3.0 m long to its other end? The area of cross-section of the wire is 2.0 × 10−6 m2 and it is carrying a current of 3.0 A.
When electrons drift in a metal from lower to higher potential, does it mean that all the free electrons of the metal are moving in the same direction?
Define relaxation time of the free electrons drifting in a conductor. How is it related to the drift velocity of free electrons? Use this relation to deduce the expression for the electrical resistivity of the material.
A current of 1.0 A exists in a copper wire of cross-section 1.0 mm2. Assuming one free electron per atom, calculate the drift speed of the free electrons in the wire. The density of copper is 9000 kg m–3.
Consider a wire of length 4 m and cross-sectional area 1 mm2 carrying a current of 2 A. If each cubic metre of the material contains 1029 free electrons, find the average time taken by an electron to cross the length of the wire.
Consider the following statements.
(A) Free-electron density is different in different metals.
(B) Free-electron density in a metal depends on temperature.
Seebeck Effect is caused _____________ .
Consider the following statements.
(A) Free-electron density is different in different metals.
(B) Free-electron density in a metal depends on temperature.
Peltier Effect is caused _______________ .
Obtain the expression for the current flowing through a conductor having number density of the electron n, area of cross-section A in terms of the drift velocity vd .
When a current I is set up in a wire of radius r, the drift velocity is vd· If the same current is set up through a wire of radius 2 r, the drift velocity will be:
An electric bulb.is rated 220 v and 100 watt power consumed by it when operated on 'no volt is:-
The drift velocity of a free electron inside a conductor is ______
Is the momentum conserved when charge crosses a junction in an electric circuit? Why or why not?
- Consider circuit in figure. How much energy is absorbed by electrons from the initial state of no current (ignore thermal motion) to the state of drift velocity?
- Electrons give up energy at the rate of RI2 per second to the thermal energy. What time scale would one associate with energy in problem (a)? n = no of electron/volume = 1029/m3, length of circuit = 10 cm, cross-section = A = (1mm)2
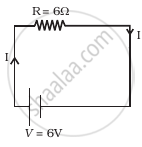
Derive an expression for resistivity of a conductor in terms of the number density of charge carriers in the conductor and relaxation time.
