Advertisements
Advertisements
प्रश्न
A current of 1.0 A exists in a copper wire of cross-section 1.0 mm2. Assuming one free electron per atom, calculate the drift speed of the free electrons in the wire. The density of copper is 9000 kg m–3.
उत्तर
Given:-
Current, i = 1 A
Area of cross-section, A = 1 mm2 = 1 × 10–6 m2
Density of copper,
ρ = 9000 kg/m3
Length of the conductor = l
Also,
Mass of copper wire = Volume × density
\[\Rightarrow m = A \times l \times \rho\]
\[ \Rightarrow m = A \times l \times 9000 kg\]
We know that the number of atoms in molecular mass M = NA
∴ Number of atoms in mass m, N = \[\left( \frac{N_A}{M} \right)m\]
where NA is known as Avagadro's number and is equal to 6 × 1023 atoms.
\[\Rightarrow N = \left( \frac{N_A}{M} \right)m\]
\[ \Rightarrow N = \left( \frac{N_A}{M} \right) \times A \times l \times 9000\]
Also, it is given that
No. of free electrons = No. of atoms
Let n be the number of free electrons per unit volume
\[n = \frac{\text{Number of electrons}}{\text{Volume}}\]
\[ = \frac{N_A \times A \times l \times 9000}{M \times A \times l}\]
\[ = \frac{N_A \times 9000}{M}\]
\[ = \frac{6 \times {10}^{23} \times 9000}{63 . 5 \times {10}^{- 3}}\]
\[ \therefore i = V_d nAe\]
\[ \Rightarrow V_d = \frac{1}{\frac{6 \times {10}^{23} \times 9000}{63 . 5 \times {10}^{- 3}} \times {10}^{- 6} \times 1 . 6 \times {10}^{- 19}}\]
\[ = \frac{63 . 5 \times {10}^{- 3}}{6 \times {10}^{23} \times 9000 \times {10}^{- 6} \times 1 . 6 \times {10}^{- 19}}\]
\[ = \frac{63 . 5 \times {10}^{- 3}}{6 \times {10}^{26} \times 9 \times {10}^{- 6} \times 1 . 6 \times {10}^{- 19}}\]
\[ = \frac{63 . 5 \times {10}^{- 3}}{6 \times 9 \times 16}\]
\[ = 0 . 073 \times {10}^{- 3}\text{ m/s} \]
\[ = 0 . 073\text{ mm/s}\]
APPEARS IN
संबंधित प्रश्न
Estimate the average drift speed of conduction electrons in a copper wire of cross-sectional area 1.0 × 10−7 m2 carrying a current of 1.5 A. Assume the density of conduction electrons to be 9 × 1028 m−3
Estimate the average drift speed of conduction electrons in a copper wire of cross-sectional area 2·5 × 10−7 m2 carrying a current of 2·7 A. Assume the density of conduction electrons to be 9 × 1028 m−3
The number density of free electrons in a copper conductor is 8.5 × 1028 m−3. How long does an electron take to drift from one end of a wire 3.0 m long to its other end? The area of cross-section of the wire is 2.0 × 10−6 m2 and it is carrying a current of 3.0 A.
(a) drift speed
(b) current density
(c) electric current
(d) electric field
On the basis of electron drift, derive an expression for resistivity of a conductor in terms of number density of free electrons and relaxation time. On what factors does resistivity of a conductor depend?
Define relaxation time of the free electrons drifting in a conductor. How is it related to the drift velocity of free electrons? Use this relation to deduce the expression for the electrical resistivity of the material.
Derive an expression for drift velocity of free electrons in a conductor in terms of relaxation time.
When a current is established in a wire, the free electrons drift in the direction opposite to the current. Does the number of free electrons in the wire continuously decrease?
Electrons are emitted by a hot filament and are accelerated by an electric field, as shown in the figure. The two stops at the left ensure that the electron beam has a uniform cross-section.
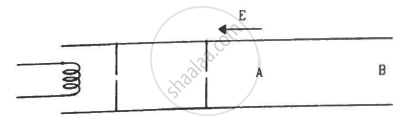
Consider a wire of length 4 m and cross-sectional area 1 mm2 carrying a current of 2 A. If each cubic metre of the material contains 1029 free electrons, find the average time taken by an electron to cross the length of the wire.
Consider the following statements.
(A) Free-electron density is different in different metals.
(B) Free-electron density in a metal depends on temperature.
Seebeck Effect is caused _____________ .
At room temperature, copper has free electron density of 8.4 × 1028 per m3. The copper conductor has a cross-section of l0−6 m2 and carries a current of 5.4 A. The electron drift velocity in copper is:
Metals are good conductor of heat than insulator because
The drift velocity of a free electron inside a conductor is ______
Derive an expression for resistivity of a conductor in terms of the number density of charge carriers in the conductor and relaxation time.
Explain how free electrons in a metal at constant temperature attain an average velocity under the action of an electric field. Hence, obtain an expression for it.
A potential difference (V) is applied across a conductor of length 'L' and cross-sectional area 'A'.
How will the drift velocity of electrons and the current density be affected if another identical conductor of the same material were connected in series with the first conductor? Justify your answers.
