Advertisements
Advertisements
प्रश्न
The number density of free electrons in a copper conductor is 8.5 × 1028 m−3. How long does an electron take to drift from one end of a wire 3.0 m long to its other end? The area of cross-section of the wire is 2.0 × 10−6 m2 and it is carrying a current of 3.0 A.
उत्तर
Number density of free electrons in a copper conductor, n = 8.5 × 1028 m−3
Length of the copper wire, l = 3.0 m
Area of cross-section of the wire, A = 2.0 × 10−6 m2
Current carried by the wire, I = 3.0 A, which is given by the relation,
I = nAeVd
Where,
e = Electric charge = 1.6 × 10−19 C
Vd = Drift velocity =`"Length of the wire (l)"/"Time taken to cover l(t)"`
I = `"nAe""l"/"t"`
t = `"nAel"/"I"`
= `(3 xx 8.5 xx 10^28 xx 2 xx 10^-6 xx 1.6 xx 10^-19)/3.0`
= 2.7 × 104 s
Therefore, the time it takes for an electron to drift from one end of the wire to the other is 2.7 × 104 s.
APPEARS IN
संबंधित प्रश्न
Define the term drift velocity.
Derive an expression for drift velocity of free electrons.
Estimate the average drift speed of conduction electrons in a copper wire of cross-sectional area 1.0 × 10−7 m2 carrying a current of 1.5 A. Assume the density of conduction electrons to be 9 × 1028 m−3
Explain the term ‘drift velocity’ of electrons in conductor. Hence obtain the expression for the current through a conductor in terms of ‘drift velocity’.
When electrons drift in a metal from lower to higher potential, does it mean that all the free electrons of the metal are moving in the same direction?
Derive an expression for drift velocity of free electrons in a conductor in terms of relaxation time.
A current of 1.0 A exists in a copper wire of cross-section 1.0 mm2. Assuming one free electron per atom, calculate the drift speed of the free electrons in the wire. The density of copper is 9000 kg m–3.
Consider the following statements.
(A) Free-electron density is different in different metals.
(B) Free-electron density in a metal depends on temperature.
Peltier Effect is caused _______________ .
Obtain the expression for the current flowing through a conductor having number density of the electron n, area of cross-section A in terms of the drift velocity vd .
The position-time relation of a particle moving along the x-axis is given by x = a - bt + ct2 where a, band c are positive numbers. The velocity-time graph of the particle is ______.
At room temperature, copper has free electron density of 8.4 × 1028 per m3. The copper conductor has a cross-section of l0−6 m2 and carries a current of 5.4 A. The electron drift velocity in copper is:
The identical conductors maintained at same temperature are given potential difference in the ratio 1 : 2. Then the ratio of their drift velocities is ______.
- Consider circuit in figure. How much energy is absorbed by electrons from the initial state of no current (ignore thermal motion) to the state of drift velocity?
- Electrons give up energy at the rate of RI2 per second to the thermal energy. What time scale would one associate with energy in problem (a)? n = no of electron/volume = 1029/m3, length of circuit = 10 cm, cross-section = A = (1mm)2
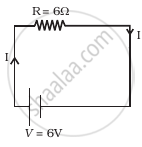
Derive an expression for resistivity of a conductor in terms of the number density of charge carriers in the conductor and relaxation time.
A potential difference (V) is applied across a conductor of length 'L' and cross-sectional area 'A'.
How will the drift velocity of electrons and the current density be affected if another identical conductor of the same material were connected in series with the first conductor? Justify your answers.
The drift velocity of electrons in a conductor connected to a battery is given by vd = `(−"eE" τ)/"m"`. Here, e is the charge of the electron, E is the electric field, τ is the average time between collisions and m is the mass of the electron.
Based on this, answer the following:
- How does the drift velocity change with a change in the potential difference across the conductor?
- A copper wire of length 'l' is connected to a source. If the copper wire is replaced by another copper wire of the same area of cross-section but of length '4l', how will the drift velocity change? Explain your answer.
